

|
|
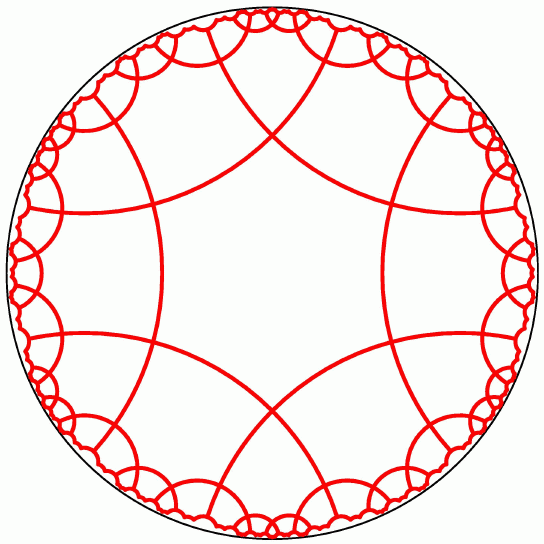
To explain how Escher came to be shocked, we go back a few years earlier to the 1954 International Congress of Mathematicians, where Coxeter and Escher first met. This led to friendship and correspondence. A couple of years after their first meeting, Coxeter wrote Escher asking for permission to use some of his striking designs in a paper in symmetry, Crystal Symmetry and Its Generalizations (published in the Transactions of the Royal Society of Canada in 1957). As a courtesy, Coxeter sent Escher a copy of that paper containing a figure with a hyperbolic tessellation just like that in Figure 1 above (in addition to Escher's designs). Escher was quite excited by that figure, since it showed him how to solve a problem that he had wondered about for a long time: how to create a repeating pattern within a limiting circle, so that the basic subpatterns or motifs became smaller toward the circular boundary. Escher wrote back to Coxeter telling of his "shock" upon seeing the figure, since it showed him at a glance the solution to his long-standing problem.
Escher, no stranger to straightedge and compass constructions,
was able to reconstruct the circular arcs in Coxeter's figure.
He put these constructions to good use
in creating his first circle limit pattern,
Circle Limit I which he included with his letter to Coxeter.
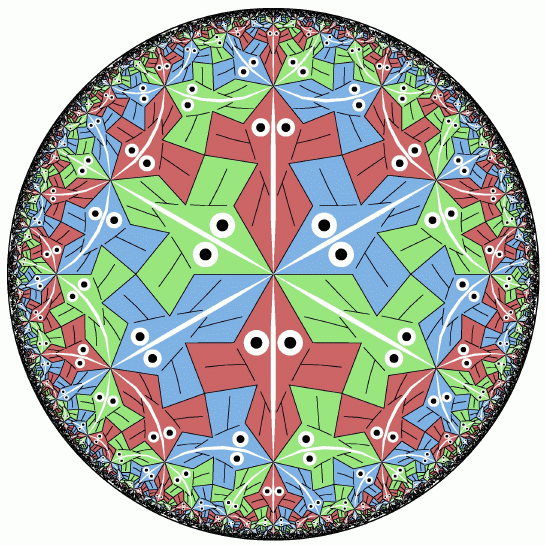
Figure 2 below is a rough computer rendition of that pattern, showing
interior details for a few of the fish.
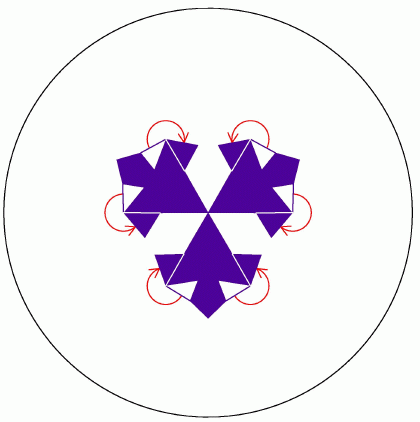
It is easy to see that Figures 1 and 2 are related.
Here is how Escher might have created Circle Limit I from
Figure 1.
First switch the colors of half the triangles of Figure 1 so that triangles
sharing a hypotenuse have the same color.
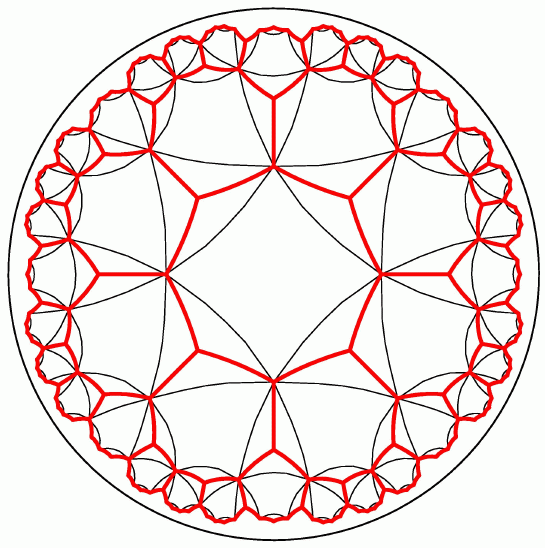
The result is a pattern of "kites", as shown in Figure 3 below.
Next, remove small triangular pieces from each of the
short sides of the black kites and paste them onto the long sides.
Figure 4 shows the result of doing this for just the central kites.
This produces the outlines of the black fish in
Circle Limit I.
The outlines of the white fish are formed by the holes between the black fish.
Finally, the pattern of Circle Limit I can be reconstructed by
filling in the interior details such as the eyes and backbones of the fish.
The points of the Poincaré disk model of hyperbolic geometry
are the interior points of a bounding circle in the Euclidean plane.
In this model,
hyperbolic lines are represented by circular arcs that are
perpendicular to the bounding circle, including diameters.
Figures 1 and 2 show examples of these perpendicular circular arcs.
Equal hyperbolic distances are represented by ever smaller Euclidean
distances as one approaches the bounding circle. For example, all
the triangles in Figure 1 are the same hyperbolic size, as are all the
black fish (or white fish) of Figure 2, and the kites of Figure 3.
The patterns of Figures 1, 2, and 3
are closely related to the regular hyperbolic tessellation
{6,4} shown in Figure 5 below. In general, {p,q}
denotes the regular
tessellation by regular p-sided polygons with q of them
meeting at each vertex.
Some of Escher's criticisms could be overcome by basing the
fish pattern on the {6,6} tessellation, as shown in Figure 6 below.
In fact, Figure 6 can be recolored in three colors to give it
color symmetry, which means that every symmetry (rotation, reflection, etc.)
of the uncolored pattern exactly permutes the colors of the fish in the
colored pattern.
Figure 7 shows that 3-colored pattern,
which addresses all of Escher's criticisms except for the
rectilinearity of the fish.
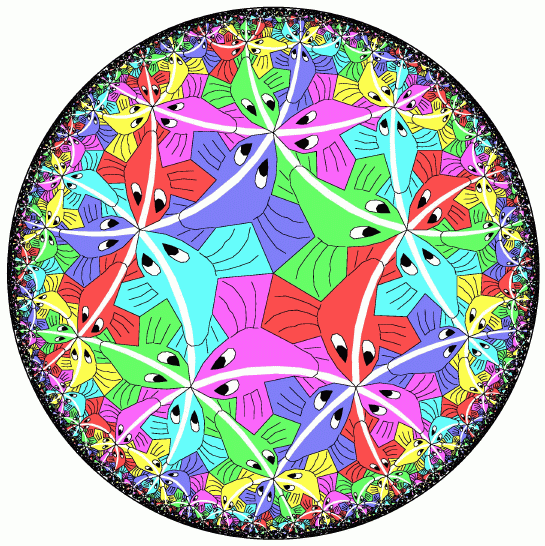
Escher never publicly explained how he designed Circle Limit III
but here is how he might have gone about it.
From his correspondence with Coxeter, Escher knew that regular
hyperbolic tessellations {p,q}
existed for any p and q satisfying
(p-2)(q-2) > 4.
In particular, he had used the {8,3} tessellation as the basis for
his second hyperbolic pattern, Circle Limit II, and
he decided to use that tessellation again for Circle Limit III.
The {8,3} tessellation is shown by the heavy lines in Figure 8 above
and in red in Figure 9 below.
Here is one way to get from the {8,3} tessellation to Circle Limit III.
First, connect alternate vertices of the octagons with
slightly curved arcs, which are shown as light arcs in Figure 9.
This divides up the hyperbolic plane into
"squares" and "equilateral" triangles.
Then if we orient the arcs by putting arrowheads on one end, we get
the paths of the fish in Circle Limit III.
This is shown in Figure 10.
A number of years ago when I was trying to figure out how to encode
the color symmetry of Circle Limit III in my computer program, I drew
a colored version of Figure 10.
Later, in 1998, it was my turn to be "shocked"
at the Centennial Exhibition of Escher's works
when I saw a colored sketch
of arrows by Escher just like mine!
He had used his drawing in preparation for Circle Limit III.
In the
Poincaré
model, equidistant curves are represented by circular arcs that
intersect the bounding circle in acute (or obtuse) angles.
Points on such arcs are an equal hyperbolic distance from the
hyperbolic line with the same endpoints on the bounding circle.
For any acute angle and hyperbolic line, there are two equidistant
curves ("branches"), one on each side of the line, making that
angle with the bounding circle.
Equidistant curves are the hyperbolic analog of small circles in
spherical geometry. For example, every point on a small circle of
latitude is an equal distance from the equatorial great circle;
and there is another small circle in the opposite hemisphere the same
distance from the equator.
Each of the backbone arcs in Circle Limit III
makes the same angle omega with the bounding circle.
Coxeter used hyperbolic trigonometry to show that
omega is given by the following expression:
Here is my analysis of Circle Limit III fish patterns:
one can imagine a three parameter family (k,l,m)
in which k right fins, l left fins, and m noses
meet, where m must be odd so that the fish swim head to tail.
The pattern would be hyperbolic, Euclidean, or spherical depending on
whether
1/k + 1/l + 1/m
is less than, equal to, or greater than 1.
Circle Limit III would be denoted (4,3,3) in this system.
Escher created a Euclidean pattern in this family, his
notebook drawing number 123, denoted (3,3,3), in which each fish
swims in one of three directions.
The pattern on the 2003 Math Awareness Month poster is (5,3,3) in this system,
and is shown below in Figure 11.
There are illuminating quotes from Escher's
correspondence with H. S. M. Coxeter in Coxeter's paper
"The non-Euclidean symmetry of Escher's
Picture `Circle Limit III'," Leonardo 12 (1979), 19-25, 32,
which also shows Coxeter's calculation of the angle of intersection of
the white arcs with the bounding circle in Circle Limit III.
Read about
artists who have been inspired by Escher and are currently creating
new mathematical "Escher" art
in the book M. C. Escher's Legacy: A Centennial Celebration,
Doris Schattschneider and Michele Emmer, editors,
Springer Verlag, 2003.
Euclidean and Non-Euclidean Geometries,
Marvin Greenberg,
3rd Edition, W. H. Freeman and Co., 1993,
has a good account of the history of
hyperbolic geometry and the
Poincaré disk model.
If you want to construct your own hyperbolic tessellation by classical
methods, see
"Compass and straightedge in the Poincaré disk,"
Chaim Goodman-Strauss,
Amer. Math. Monthly, 108 (2001), no. 1, 38-49;
to do it by computer, see
"Hyperbolic symmetry," Douglas Dunham,
Computers and Mathematics with Applications,
Part B 12 (1986), no. 1-2, 139-153.


A Bit of Hyperbolic Geometry
Mathematicians, and geometers in particular, will recognize the
patterns of the figures above as "living in" the
Poincaré disk model of hyperbolic geometry.
Escher probably knew this, but wasn't concerned about it since
he could use Euclidean constructions to build his patterns.
The fact that Poincaré's disk model can be defined in
purely Euclidean terms shows that hyperbolic geometry is
just as consistent as Euclidean geometry.
But that is another story.
Escher's Criticisms of Circle Limit I
Escher had several criticisms of his Circle Limit I pattern.
First, the fish are "rectilinear", instead of having the curved outlines of
real fish. Also, there is no "traffic flow" along the backbone lines
- the fish change directions after two fish, and the fish change
colors along lines of fish.
Another criticism, which Escher didn't make, is the pattern does not
have color symmetry since the black and white fish are not congruent.
Before reading further, look back at Figure 2 and try to
see why this is true.
There are several differences in the shapes of the black and
white fish; the most obvious is the difference in their nose angles.

Escher's Solution: Circle Limit III
Escher could have used the methods above to overcome his criticisms,
but he didn't. Escher took a different route, which led to his
beautiful print Circle Limit III.
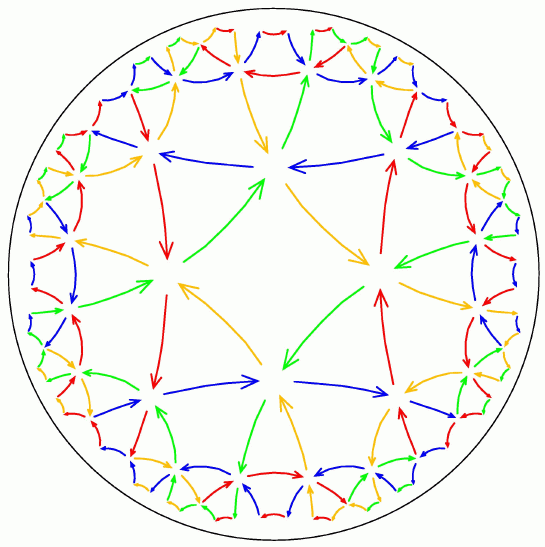
Figure 8 below shows an approximate computer-generated version of
the Circle Limit III pattern and the {8,3} tessellation
(heavy black arcs) upon which it is based.

A Bit More Hyperbolic Geometry
It is tempting to guess that the white backbone lines in Figure 8
are hyperbolic
lines (i.e. circular arcs perpendicular to the bounding circle).
But careful measurements
of Circle Limit III show that all the white arcs make angles of
approximately 80 degrees with the bounding circle.
This is as it should be, since the backbone arcs are not hyperbolic lines,
but equidistant curves, each point of which is an equal
hyperbolic distance from a hyperbolic line.
The 2003 MAM Poster Pattern
Much as Escher was inspired by Coxeter's figure, I was inspired
by Escher's "Circle Limit" patterns to create a program that
could draw them.
More than 20 years ago
two students, David Witte and John Lindgren, and I succeeded in
writing such a program.
Having gone to all the trouble to design a program that was
more general than we needed to accomplish our goal, we put it to
other uses.
Circle Limit III is certainly Escher's most stunning
hyperbolic pattern, so we thought it would be interesting to
find related patterns.
Summary
Over a period of five decades, a series of
mathematical inspirations and "shocks" have led from
from Coxeter's Figure 7 to the 2003 Math Awareness Month poster.
Many people have been inspired by Escher's work, including
the authors of articles in the recent book M. C. Escher's Legacy.
My article and electronic file on the CD Rom that accompanies
that book contain a number of other examples of computer-generated
hyperbolic tessellations inspired by Escher's art.
I only hope that the reader has as many enjoyable
inspirations and "shocks" in his or her mathematical investigations.
For Further Reading
Acknowledgement
I would like to thank Doris Schattschneider for her considerable help,
especially with the history of Escher and Coxeter's correspondence.
Page URL: http://www.d.umn.edu
/~ddunham/mathhoriz/paper.html
Page Author: Doug Dunham
Last Modified: Saturday, 01-Feb-2003 17:37:56 CST
Comments to: ddunham@d.umn.edu