The Maximum Flow Problem
There are a number of real-world problems that can be modeled as flows
in special graph called a flow network.
a flow network is a directed graph whose edges are labeled with
non-negative numbers representing a capacity for a flow of some kind:
electrical power, manufactured goods to be distributed, or city water
distribution.
The diagram below is an abstract example of a flow network.

A flow network can have special vertices called sources and
sinks.
-
A source generates or produces whatever is flowing in the
network.
The "+" vertex is intended as a source in the above flow
network.
Depending on the exact nature of the problem, a source may also have a
limit or capacity.
-
A sink consumes whatever is flowing in the network.
The "-" vertex is intended as a sink in the above flow
network.
Depending on the exact nature of the problem, a sink may also have a
limit or capacity.
Any number of vertices can be either sources or sinks, or both.
However, there are standard techniques for representing a flow network
in a form that has only one source and only one sink.
Given flow capacities along the edges, it is often useful to be able to
determine the maximum flow that can be supported by the network.
There is a general path-based algorithm, the Floyd-Fulkerson algorithm,
for solving the maximal flow problem.
A specialization of this algorithm, the Edmonds-Karp algorithm, has good
run time.
Flows
A flow in a flow network is an assignment of actual flow values
(non-negative numbers) for each of its edges.
There two restrictions:
-
The flow value for an edge is non-negative and does not exceed the
capacity for the edge.
-
The conservation rule: at each vertex other than a sink or a source,
the flows out of the vertex have the same sum as the flows into the
vertex.
The following is a possible flow in the flow network presented earlier.
The labeling on the edges has the form
actual flow value/flow capacity.
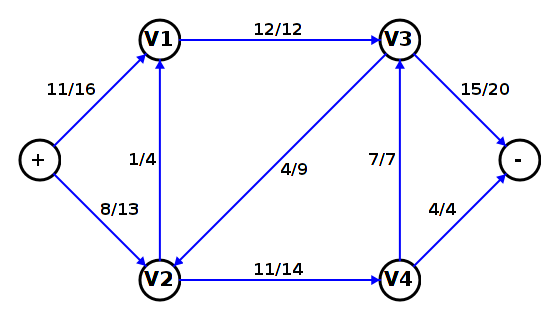
Since there is no indication of source or sink capacity, these values
are assumed to be unlimited.
But is this an optimal flow?
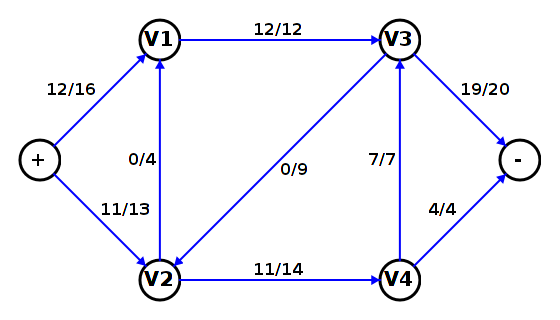
A Better Flow
The flow below improves the total flow from source to sink.
Can you do better?
Path Algorithms for Maximal Flows
The Floyd-Fulkerson algorithm works as follows.
Set initial flow values to 0.
while true
Search the reduced capacity graph for an augmenting path from "+" to "-".
If there is no augmenting path then break out of the loop.
Determine the minimum reduced capacity RCmin for edges
in the augmenting path.
Increment the flow value for each edge in the augmenting path by
RCmin.
end while
The reduced capacity graph has two edges for each edge in the
original capacity graph: one in the same direction and one reversed.
The capacity for forward edge is reduced by the flow value for the
original edge.
The capacity for the reversed edge is the value of the flow for the
original edge.
The reversed edge allows the algorithm to back out of flows used
earlier.
In the augmenting path search, edges with capacity 0 are ignored.
This ensures that RCmin is always strictly positive
until the loop terminates.
The Edmonds-Karp algorithm is a specialization of the above algorithm.
It just uses a breadth-first search to find the augmenting path.
SECTION_HEADER
Section overview text.


