The All-Pairs Shortest Paths Problem
The all-pairs shortest paths (APSP) problem is to find shortest paths
between all pairs of vertices in a graph.
There is a simple form for the solution that records a minimal amount of
information needed to lookup distances along shortest paths as well as
reconstruct the shortest paths.
There are some simple but inefficient algorithms to solve the APSP
problem.
The Floyd-Warshall agorithm gives a more efficient solution.
Assumption
For this presentation it is assumed that all edge weights are
non-negative.
There are two inefficient ways of solving the APSP:
-
Run a single-source shortest paths (SSSP) algorithm from each vertex.
This has run time O(V*E*log(E)).
If the graph has a lot of edges
(that is E = Ω(V2))
then the run time is O(V3*log(V)).
-
Use a variation of a matrix multiplication algorithm to compute the
(V - 1)-st power of the adjacency matrix.
This can be done with O(lg(V)) matrix "multiplications",
each taking O(V3) time.
Then the overall run time is again O(V3*log(V)).
The Floyd-Warshall algorithm
initialize pathInfo matrix using only paths with no intermediate vertices
for each vertex k
// Invariant:
// For every i and j, pathInfo[i][j] describes the shortest path from
// i to j among paths whose intermediate vertices are all less than k.
for each vertex i
for each vertex j
update pathInfo[i][j] to allow for using k as an intermediate vertex
end for
end for
end for
The following is the invariant for the outermost loop:
For every i and j, pathInfo[i][j] describes the shortest path from
i to j among paths whose intermediate vertices are all less than k.
Initialization code should be designed to establish the invariant for
k = 0.
In other words, pathInfo[i][j] initially describes the
shortest path from i to j that has no intermediate vertices.
The paths we are considering have at most one edge.
If i == j (no edges) then
-
pathInfo[i][i].distance should be set to 0
and
-
pathInfo[i][i].neighbor should be set to
null.
If there is an edge of weight w from vertex i
to vertex j (one edge) then
-
pathInfo[i][j].distance should be set to
w and
-
pathInfo[i][j].neighbor should be set to
j.
Otherwise
-
pathInfo[i][j].distance should be set to
Double.POSITIVE_INFINITY and
-
pathInfo[i][j].neighbor should be set to
null.
Floyd-Warshall Update
The following is the invariant for the outermost loop:
For every i and j, pathInfo[i][j] describes the shortest path from
i to j among paths whose intermediate vertices are all less than k.
Update code assumes the invariant is true for the current value of k.
The code should be designed to establish the invariant for k + 1.
This ensures that the invariant is true at the beginning of the next
iteration of the outermost loop.
The update is suggested by the following diagram.
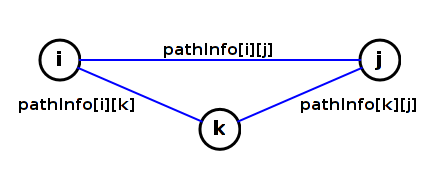
Here, we are trying to update pathInfo[i][j].
If pathInfo[i][j].distance <
pathInfo[i][k].distance +
pathInfo[k][j].distance then allowing k to be
used as an intermediate vertex yields a shorter path.
Then the update should change pathInfo[i][j]:
-
pathInfo[i][j].distance is set to
pathInfo[i][k].distance + pathInfo[k][j].distance
-
pathInfo[i][j].neighbor is set to
pathInfo[i][k].neighbor
Otherwise pathInfo[i][j] should not be changed.
Note that following these rules does not lead to an update of
either pathInfo[i][k] or pathInfo[k][j].
The loop does not need special case code to deal with these cases.
Floyd-Warshall Run Time
The Floyd-Warshall run time is O(V3).
