The software supplement to the book Contemporary Abstract Algebra, 5th edition, 2002, Houghton Mifflin by Joseph A. Gallian was begun by Arvind Rajagopal in 1997 for his M.S. project. Over the years the software supplement was improved and expanded by Xiong Wang, Kai Xu and Dong Liang.
The computer exercises are meant to allow students to produce data,explore
examples, and make and test conjectures.
![]()
A typical program( Applet ) looks like this.....
- a. The elements of U(n).
- b. The inverse of each member of U(n). ( Please go ahead and try it!! )
I have used a "Text Field" to accept values from the users and a "Scrollable Canvas" to display the solutions. I have also provided a "clear button" to refresh the canvas. I plan to provide a "print button" to print the contents of the canvas, later.
Having seen how a typical Applet works let me take you into the design of the whole program. All the programming exercises use two packages that I built called algebra and misc( has miscellaneous items like Scrollable Canvas, Text Field, and other Utilitiy functions ). Typically, each trial is considered as an algebra.answer and algebra.answers are made of either a algebra.sentence or a algebra.table. Both algebra.sentence and algebra.table are subclasses of the abstract class algebra.entity and implement an interface algebra.Drawable that enables them to draw themselves on the canvas.
- public void draw( Graphics g, integer W, integer H,
- integer X, integer Y );.
- Once the user enters a value in the text field, it is read using Integer.parseInt. Exceptions, if there are any, are handled and the value is passed to the relevant method in the application applet.
- Inside the method calculations are performed and entitys are built one at a time. That is, an answer is built line by line. Once the method fills a line( which is an algebra.entity ) it invokes the paint() method of misc.ScrollableCanvas which appends the entity to the current answer. This process goes on till the end of the solution.
- Once the calculations are done the newanswer() method of misc.ScrollableCanvas is invoked, which increments the answer count by one and invokes the paint method of Mycanvas which is a sub-class of java.awt.Canvas and defined inside misc.ScrollableCanvas.
- Inside the paint () method of Mycanvas, answers ( various trials ) are read one by one. With each answer 's get_line() method the entities( sentence or table ) are retrieved and instantiated as an algebra.Drawable. Since Drawable defines a draw() method, which is given above, and since each of the Words know how to draw themselves, the answer's are painted on the canvas. The key is that the Graphics object of the paint() method in Mycanvas is passed by reference to the Words and hence the painting is achieved by invoking the draw() method in each Word(s).
Here's the diagramatic representation of the algebra package:
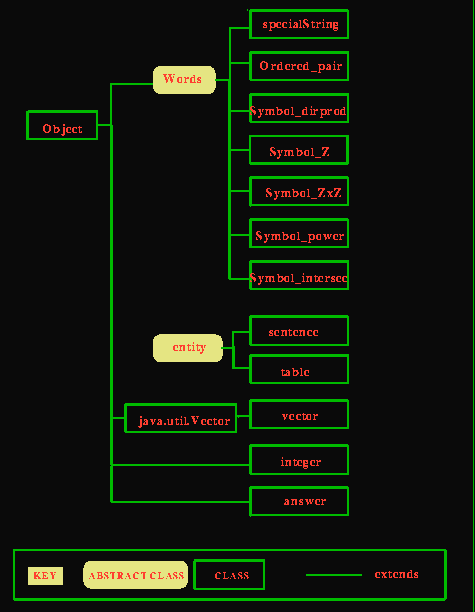
All subclasses of algebra.Words and algebra.entity implement the interfaces algebra.Drawable and Cloneable. Also the interface Drawable is a part of the package algebra.
Both algebra.sentence and algebra.table are composed of algebra.Words. As you can see, there are seven kinds of Words. All subclasses of algebra.Words implement the algebra.Drawable interface and hence can draw themselves.
The algebra.Drawable interface has just one method draw() which is defined as follows:
Where 'g' is a 'Graphics' object while W, H, X, and Y, which stand for the width, height, x-coordinate and y-coordinate respectively, are of the type algebra.integer which is just a wrapper to an 'int' with some extra functionalities.
If we call the individual problems( programming exercises ) as 'application applets', here's how the application applets work.
Please take a look at the packages algebra and misc.
![]()