One of the first approaches developed to systematically handle non-tonal materials involves intervallically related, yet unordered groups of pitches. These groups would later be afforded the term sets by theorists drawing from a branch of mathematics. The early non-tonal compositions of Arnold Schönberg (1874-1951), such as The Book of the Hanging Gardens (op.15), and Anton Webern (1883-1945), such as the Six Bagatelles for String Quartet (op.9), implement this method with great variety in terms of technique and expression. Although Schönberg was to further develop this approach into dodecaphony, the use of sets seems to have been adopted by more composers, and even integrated into quasi-tonal composition, such as in Frederic Rzewski's (b. 1938) The People United Will Never Be Defeated!. While dodecaphony has had less of an impact on contemporary compositional thought, organization of materials through the use of sets remains pertinent.
In order to understand the principles governing composition using sets, we must begin by referring to intervals as a graded absolute rather than in relation to the major and minor scales from which they are no longer associated. For instance, a minor second contains within its compass one chromatic step, while a major second contains two. Therefore, in an absolute system, they can be identified simply as 1 and 2 in a system of 12 steps.
Based on this premise, when placing a pitch in context with another pitch, we need to speak about them in terms of the initial pitch (which contains no steps) in relation to how many steps away the other pitch lies, notwithstanding the placement of the second pitch as being higher or lower: an absolute relation. For example, if we take the two pitches C and Bb, the closest relationship between the two exists when the Bb is placed lower than the C. If C is the initial pitch (0) then Bb, being two steps away, is (2) and the relationship between the two is the set (0, 2). This set can of course be subsequently applied to any other group of two pitches with the same intervallic content, such as G#-F#, B-C#, F-Eb, C-D, etc. The important aspect for the composer is that this system can be employed to associate different musical ideas that are of the same set.
When applying set ideas to more than two pitches, we need to group them into what is referred to as normal form (the most compressed version possible, either ascending or descending). Let's begin with a pitch class set (an unordered group of notes): C, A, Db, as our initial musical idea.
We must now organize these pitches into a series of either ascending or descending pattern to determine this set's normal form. To do this, we will rotate the first note of the group and then place the other pitches in a scalar arrangement so that they don't exceed the span of an octave from lowest to highest. We will do this twice, once ascending, and then descending.
As can be observed, arrangement c. is the most compressed version, making the musical idea's set (0, 1, 4). Although arrangement f. also has a span of only 0 to 4, the internal 3 is of higher value than the content of c. which is 1.
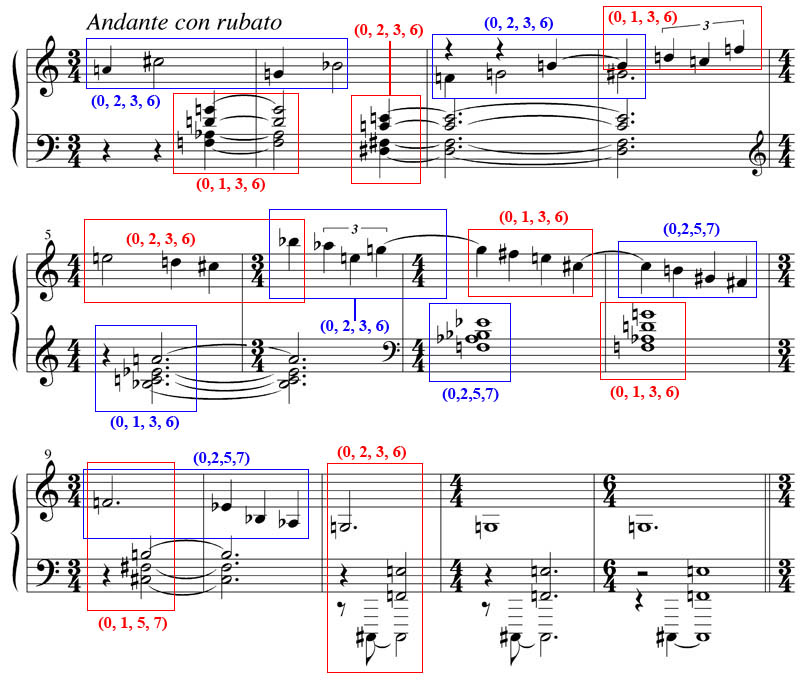
Henceforth, the composer can create other musical ideas from the set (0, 1, 4) by transposition and maintain an organic connection with the initial group. The important distinction with orthodox 12-tone music (dodecaphony) is the concept that the pitches within each group have no assigned order. The question that the composer must pose is whether to begin first with a musical idea from which to derive a set or the other way around. As well, how many different sets should be used during the course of a piece to create contrast while maintaining comprehension within the context of a non-tonal composition is equally important. The answers to these questions lies within the creative concerns of the individual. In our brief original composition below, we will explore the application of selected fundamental set techniques.