1. BRIEFLY define the following terms and give an example of how each term is used: (4 each, no more than six on the midterm)
   • Interpreter
   • Compiler
   • Scanner
   • Parser
   • Lexeme
   • Token
   • Nondeterministic Finite State Machine
   • Deterministic Finite State Machine
   • Regular Expression
   • Transducer
   • Context-Free Grammar
   • Language
   • Parse Tree
   • Top-Down Parsing
   • Bottom-Up Parsing
   • Terminal
   • Non-terminal
   • Production
   • Derivation
   • Left-Most Derivation
   • Right-Most Derivation
   • Ambiguity (in a grammar)
   • Precedence
   • Associativity
   • Right Associativity
   • Left Associativity
   • Recursive Grammar
   • Left Recursive Grammar
   • Left Factoring
   • Recursive Descent Parsing
   • Predictive Parsing
   • First Set
   • Follow Set
   • LL(1) Parser
   • Parse Table
   • Shift in LR Parser
   • Reduce in LR Parser
   • Shift-Reduce Conflict
   • Reduce-Reduce Conflict
   • Precedence Declaration
   • LR(k) Parsing

   NOTE: due to material covered in class, these terms do not apply to midterm 1:

   • SLR Parsing
   • Canonical LR(1) Tables
   • LR(0) Items
   • LALR Parsing
   • Closure of a Set of LR(0) Items
2. Diagram the likely components of a compiler and describe what each component does in the compiler. (15)
3. A legal string begins with from 1 to 3 a's, is followed by 0 or more b's, c's, or d's, and ends with at least one e. (5 each)
   1. Create a deterministic finite state machine to accept legal strings (and only legal strings).
   2. Create a nondeterministic finite state machine to accept legal strings (and only legal strings).
   3. Create a regular expression to accept legal strings (and only legal strings).
4. Briefly describe the language accepted by each of the following: (5 each)
   1. 1* 0 ( 1* 0 1* 0 1* ) *
   2. {+ abc | def }+
   3. 10* 1 | 01* 0
5. Translate the regular expression
   (a | b | c) * d (e+) f
   into a corresponding non-deterministic finite state machine. (10)
6. Using the algorithm described in class construct a deterministic finite state machine from the nondeterministic machine shown below: (15)
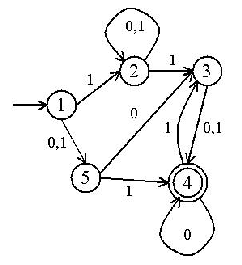
7. A language consists of the following tokens: +, +=, -, -=, =, ==, and != separated by white space consisting of spaces, tabs and newlines. Draw a picture of or create a table describing a transducer to recognize tokens in this language. Make sure to define any actions you may use in your transducer. (15)
8. Given the following grammar: (10)
   E -> E + E | E - E | E * E | E / E | - E | int
   Show two different left-most derivations of the string int + int * int / int. Also show the corresponding parse trees. What does this tell you?
9. How would you change the following grammar: (15)
   E -> E + E | E - E | E * E | E / E | - E | int
   so that all of the binary operations are left associative and the precedence of the operators is (highest to lowest): +,* (highest), /, - (middle), unary - (lowest)?
10. The following grammar is clearly not LL(1), how would you transform the grammar to make it LL(1)? (15)
    A -> A + B | A - B | B
    B -> C * B | C / B | C
    C -> ( A ) | int
11. Determine, by attempting to construct a parse table, whether the following grammar is LL(1). Make sure to show all the needed FIRST and FOLLOW sets you used to construct the parse table. (20)
    S -> A $
    A -> - A B | id C
    B -> - B | ""
    C -> "" | . id
12. Define a recursive descent parser for the following grammar using recursive functions: (15)
    S -> A $
    A -> - A B | id C
    B -> - B | ""
    C -> "" | . id
13. Define, in general terms, LR(k) parsing. Make sure to include a description of what an LR(k) parse table looks like and what are the possible actions in such a parse table. How do you know if an grammar is ambiguous for LR(k) parsing?

NOTE: due to material covered in class, these questions do not apply to midterm 1:

• Describe the relationship between a production and an item in an LR(0) grammar. How does this relate to the notion of the stack in an LR(0) grammar? Give an algorithm for constructing the closure of a set of items LR(0) with respect to a particular grammar.
• For the following grammar, construct the set of LR(0) states to recognize viable prefixes of this language. Then fill out an SLR parse table for this grammar and indicate whether the grammar is ambiguous.
  S -> A $
  A -> -- A B | ++ A B | id B
  B -> -- B | ++ B | .