Some sample exam 1 questions:

1. BRIEFLY define the following terms and give an example of how each term is used.
   • Interpreter
   • Compiler
   • Scanner
   • Parser
   • Lexeme
   • Token
   • Nondeterministic Finite Automaton
   • Deterministic Finite State Machine
   • Regular Expression
   • Transducer
   • Context-Free Grammar
   • Language
   • Parse Tree
   • Top-Down Parsing
   • Bottom-Up Parsing
   • Terminal
   • Non-terminal
   • Production
   • Derivation
   • Left-Most Derivation
   • Right-Most Derivation
   • Ambiguity (in a grammar)
   • Precedence
   • Associativity
   • Right Associativity
   • Left Associativity
   • Recursive Grammar
   • Left Recursive Grammar
   • Left Factoring
   • Recursive Descent Parsing
   • Predictive Parsing
   • First Set
   • Follow Set
   • LL(1) Parser
   • Parse Table
2. Diagram the likely components of a compiler and describe what each component does in the compiler.
3. A legal string begins with from 1 to 3 a's, is followed by 0 or more b's, c's, or d's, and ends with at least one e.
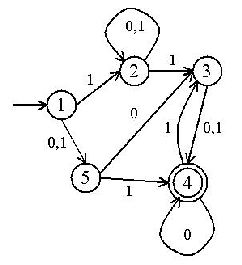
   1. Create a deterministic finite state machine to accept legal strings (and only legal strings).
   2. Create a nondeterministic finite state machine to accept legal strings (and only legal strings).
   3. Create a regular expression to accept legal strings (and only legal strings).
4. Briefly describe the language accepted by each of the following:
   1. 1* 0 ( 1* 0 1* 0 1* ) *
   2. {+ abc | def }+
   3. 10* 1 | 01* 0
5. Translate the regular expression
   (a | b | c) * d (e+) f
   into a corresponding non-deterministic finite state machine.
6. Using the algorithm described in class construct a deterministic finite state machine from the nondeterministic machine shown below:
7. A language consists of the following tokens: +, +=, -, -=, =, ==, and != separated by white space consisting of spaces, tabs and newlines. Draw a picture of or create a table describing a transducer to recognize tokens in this language. Make sure to define any actions you may use in your transducer.
8. Given the following grammar:
   E -> E + E | E - E | E * E | E / E | - E | int
   Show two different left-most derivations of the string int + int * int / int. Also show the corresponding parse trees. What does this tell you?
9. How would you change the following grammar:
   E -> E + E | E - E | E * E | E / E | - E | int
   so that all of the binary operations are left associative and the precedence of the operators is (highest to lowest): +,* (highest), /, - (middle), unary - (lowest)?
10. The following grammar is clearly not LL(1), how would you transform the grammar to make it LL(1)?
    A -> A + B | A - B | B
    B -> C * B | C / B | C
    C -> ( A ) | int
11. Determine, by attempting to construct a parse table, whether the following grammar is LL(1). Make sure to show all the needed FIRST and FOLLOW sets you used to construct the parse table.
    S -> A $
    A -> - A B | id C
    B -> - B | ""
    C -> "" | . id
12. Define a recursive descent parser for the following grammar using recursive functions:
    S -> A $
    A -> - A B | id C
    B -> - B | ""
    C -> "" | . id