The blocks world has two kinds of components: A legal move is to transfer a block from one place or block onto another place or block, with these restrictions:
Example State Representation Moves Heuristics
Here is a simple blocks world problem:

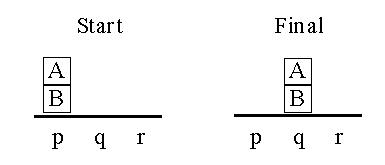
And here is its shortest solution:

A two-dimensional array may be appropriate (as in the 8-puzzle), however: Stacks are a natural structure for piles of blocks.
This section discusses blocks world move representation and its effect on the state space search space.
Move Representation Search Space
It is straightforward to think of a move in the blocks world as transferring from one place (the source) to another place (the destination).

So the name of the block is not necessary to uniquely specify a move.

The three moves used in the example (see to the left) are:

The doMove method in the blocks world move class must return null if there is no block on the source place.
The number of move objects to create is dependent on the number of places, but not on the number of blocks.

In general, if there are n places, there should be n*(n-1) move objects.

In our blocks world there are 3 places and so 6 move objects.

Since a blocks world search tree node can expand to as many as 6 children while an 8-puzzle search tree node can expand to a maximum of 4, blocks problems can generate larger search spaces.

You will need to devise an informed blocks world heuristic function.

This section discusses heuristics for the blocks world.

We show a heuristic that significantly underestimates, and one that overestimates.

Underestimating Overestimating Performance
As with the 8-puzzle, a natural heuristic to consider is the number of blocks that are out of place relative to the final state.

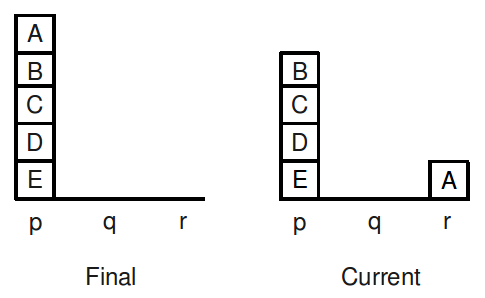
For example, in the current state below there are three blocks out of place (shown in red):

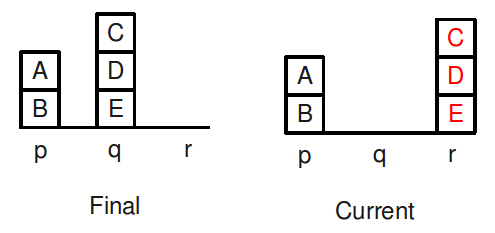
Since the actual number of moves required is five, this is not a poor estimate.

However, the heuristic is naive because it does not take into account whether a block, even if it is in the correct place, has correctly placed blocks under it, as some counterexamples show.

Example 1 Example 2
Consider this situation:

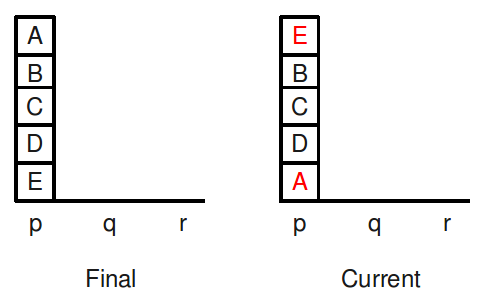
The number of blocks out of place is two, but the actual number of moves required is at least ten — five to get place p clear and at least five more to move blocks back into place.

So the heuristic underestimates considerably.

As a second example, consider:

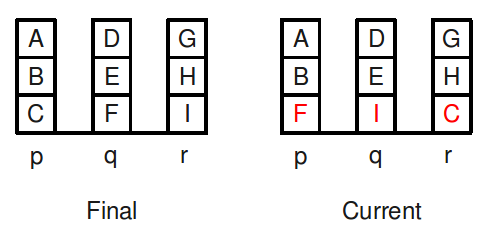
The current state has only three blocks out of place but the number of moves required is 21.

You should implement the number-of-blocks-out-of-place heuristic for testing purposes, but you should also come up with a more informed heuristic that does not overestimate.

Note that the "sum of Manhattan distances" heuristic does overestimate for the blocks world problem. Suppose:

The "Manhattan distance" of A from its destination is six, but only one move is required to get it there.

I have experimented with several blocks world heuristics: The performance of these heuristics, in terms of the number of priority queue operations and the maximum priority queue size, is shown below.

You can compare your own heuristic's performance against these.

Problem Minimum
Solution Length		 Heuristic Number of
PQ Operations		 Maximum
PQ Size
1 3 blocks out of place 17 8
more informed 17 8
very informed 17 8
2 5 blocks out of place 60 29
more informed 47 24
very informed 41 20
3 6 blocks out of place 135 74
more informed 108 57
very informed 37 20
4 8 blocks out of place 490 253
more informed 329 180
very informed 307 168
5 12 blocks out of place 55,982 33,873
more informed 17,494 10,783
very informed 314 203
6 17 blocks out of place 913,121 562,042
more informed 34,159 21,034
very informed 1,566 983
7 21 blocks out of place Heap Overflow Heap Overflow
more informed Heap Overflow Heap Overflow
very informed 642,262 394,251