A red-black tree is a binary search tree in which all nodes are
colored either red or black.
Additional conditions (invariants) impose restrictions on the
tree to ensure reasonable balance.
After looking at these invariants it is useful to examine some
operations that preserve the invariants.
These operations are useful for rebalancing.
Red-black trees satisfy three invariants:
-
The node keys are in order from left to right.
This invariant is common to all binary search trees.
It ensures that searching for a given key can be implemented
the same way regardless of the rebalancing strategy.
-
A bookkeeping invariant.
-
A balance invariant.
The last two invariants together bound the height of a tree in
terms of the number of nodes that it contains, resulting in a
significant improvement in run times for searches, inserts, and
deletes.
It is impossible to maintain the last two invariants at all
times.
However, in object-oriented programming we can make them
class invariants.
This means that
-
they are established initially in a red-black tree
constructor, and
-
all public red-black tree methods preserve the invariants.
That is, if the invariants hold before a method is invoked
then they will hold after the method returns.
Consequently, from the point of view of a red-black tree class
client the invariants are always true.
As is common in data structures, in method implementations the
class invariants are replaced by weakened invariants.
The choice of the weakened invariants depends on the method, but
usually bookkeeping invariants remain unmodified.
Even if you are messing things up you try to keep the records
straight.
All paths through the tree contain the same number of black
nodes.
This amounts to requiring that the tree be perfectly balanced,
but red nodes are ignored.
This invariant just specifies how we do bookkeeping to check for
balance.
By itself, the bookkeeping invariant has no teeth.
You can satisfy it in any binary search tree by making all of
the nodes red.
No red nodes have red parents.
This invariant adds teeth to the bookeeping invariant.
It ensures that the number of nodes, red or black, along two
paths through the tree can differ by at most a factor of at most
2.
It can be shown that the height of a red-black tree with
n nodes is O(log(n)).
In fact, the big-O constant is 2.
This implies that searches in a red-black tree have
O(log(n)) worst-case run time.
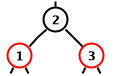
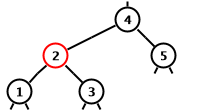
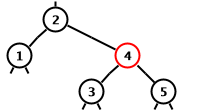
There is one important operation that can be performed on any
binary search tree: a rotation.
It preserves the left-to-right ordering invariant
It is illustrated in the diagrams below.
These diagrams only represent a portion of a binary search tree.
There also may be other nodes above the top no of the trees.
Nodes 1, 3, and 5 represent possibly empty subtrees.
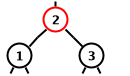
-
A right rotation from node 2 in the left diagram
results in the right diagram.
-
A left rotation from node 4 in the right diagram
results in the left diagram.
For either a left or right rotation the only changes to the tree
are references to or from nodes 2 and 4 so a rotation can be
done in constant time.
This operation needs to be modified for red-black trees to
minimize the damage done to the bookkeeping and balance
invariants.
In addition, it is useful to have a promotion operation
that modifies the bookkeeping without changing the structure of
a tree.
A red-black tree rotation is structurally the same as an
ordinary binary search tree rotation.
In addition it swaps the colors of the the "from" node (node 2
for a right rotation) and its parent (node 4 for a right
rotation).
A red-black tree rotation does not change the number of black
nodes on any paths throuh the affected region of the tree.
That is, it preserves the bookkeeping invariant.
A right red-black tree rotation is useful when node 1 is red
and node 5 is black.
Then it eliminates the balance invariant violation.
Inserts in a red-black tree add a new node with color red to
avoid violating the bookkeeping invariant.
The code for rebalancing after adding the node is just a simple
loop with the following invariants:
-
The bookkeeping invariant: all paths through the tree have
the same number of black nodes.
-
A relaxed balance invariant: there is at most one red node
that has a red parent.
The loop code attempts to either eliminate the double red or to
move it higher up in the tree. Simple cases deal with
situations where there is no double red or it can be fixed
immediately without using rotations.
Other cases use rotations or move the double red closer to the
root.
If the new red is the root then it has no parent so there is no
violation of the balance invariant.
Nothing more needs to be done.
If the parent of the new red node is not red then there is no
violation of the balance invariant.
Nothing more needs to be done.
If the parent of the new red is the root and it is red then it
can be made black.
This changes the number of blacks on all paths through the tree
by the same amount so it does not result in a violation of the
bookkeeping invariant.
It also eliminates the violation of the balance invariant.
Nothing more needs to be done.
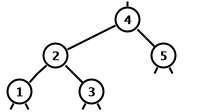
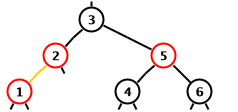
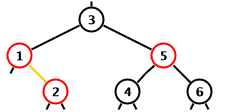
The other insert case are described by one of the two following
diagrams or their mirror images.
The new red in the left diagram, the straight chain case, is
node 1.
The new red in the right diagram, the crooked chain case, is
node 2.
We are assuming that easy case conditions did not hold so that
both the new red and its parent are red.
In either diagram the uncle is node 5.
When the uncle is red as shown below both diagrams can be
handled with the same code.
Otherwise, different code is needed for the two diagrams.
If the uncle is red then conditions for doing a promote at the
grandparent are satisfied: the grandparent is black and both of
its children are red.
The promote eliminates the balance invariant violation between
the current new red and its parent but it turns the grandparent
red. This may result in a new violation.
This can be handled by continuing the insert rebalancing loop
with the grandparent as the new red.


If the uncle is not red, including the possibility that it is
null, then a promote cannot be done.
However, if the new red, its parent, and its grandparent form a
straight chain then a rotation from the parent separates the
two reds.
This fixes the balance invariant violation so the insert
rebalancing loop can be terminated.
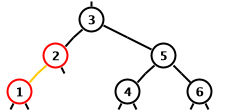
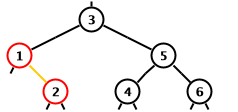
If the new red, its parent, and its grandparent form a crooked
chain then a rotation from the parent does not separate the two
reds because the new red becomes the child of the grandparent,
which turns red.
However, the chain can be straightened out first by doing a
rotation from the new red.
If the loop is continued after this rotation the the next
iteration will find a straight chain to the grandparent and it
will fix the balance invariant violation.
After a node is removed the only possible violation of the
red-black tree invariants is a violation of the bookkeeping
invariant.
More precisely, a path through the link to the removed node may
have one fewer black nodes than other paths.
There are two quick fixes that deal with cases that do not
require a loop to restore the bookkeeping invariant.
Otherwise a rebalancing loop is required.
There are two delete cases that can be handled without a loop:
-
The removed node is red.
Then there is nothing to be done.
Removal of the node did not violate either of the red-black
tree invariants.
-
The node at the end of the removal link is red.
This happens when the removed node has exactly one child.
This child must be red.
When the removed node was removed the red child took its
place.
There is a violation of the bookkeeping invariant since the
removed node must be black.
The violation can be fixed by changing the color of the red
child to black.
If neither of the quick fixes applies then paths through the
removal link are short by one black node compared to the
pre-delete situation.
We refer to this kind of link as a pale link.
The delete rebalancing loop maintains the following invariants:
-
A relaxed bookkeeping invariant: all violations of the
bookkeeping invariant can be accounted for by a single pale
link.
All paths through this link are short by one black node.
-
The balance invariant: no red node has a red parent.
One of the loop cases, when the pale link is at the root, is
trivial to handle.
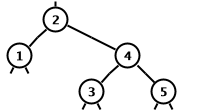
Otherwise the cases can be classified by colors occurring in the
following diagram or its mirror image:
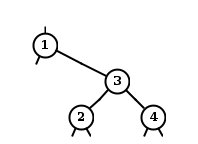
The cases are described using the following terminology.
-
The pale link is the left link from node 1.
-
The parent node is node 1.
-
The sibling node is node 3.
-
The near niece node is node 2, the closest child of the
sibling node.
-
The far niece node is node 4, the furthest child of the
sibling node.
Links are named according to their end nodes.
For example, the far niece link is the link from the sibling
node to the far niece node.
The order of the cases in the menu to the left is important.
Cases are named by a single condition but other conditions may
be required for the case.
These additional conditions are implied by failure to satisfy
conditions for earlier cases.
If the pale link is the root link then all paths through the
tree are short by one black node compared to the pre-delete
situation.
But this means that all paths through the tree have the same
number of black nodes so the red-black tree invariants have
been reestablished. Nothing more needs to be done.
A check for the negation of this condition can be used as a loop
continuation condition.

Conditions assumed from failure of earlier case conditions: the
pale link is not the root link so the pale link has a sibling.
If the sibling is red then we can do a rotation at the sibling
link.
This does not fix the pale link but it makes its parent red so
one of the other cases will apply on the next iteration of the
loop.

Conditions assumed from failure of earlier case conditions: the
pale link is not the root link so the pale link has a sibling.
Then the niece links exist though their end nodes may be null.
If the far niece is red then we do three things:
-
Swap colors across the far niece link.
This makes the near niece link pale.
-
Rotate the sibling link.
This makes both of the pale links children of the same red
node, the start of the original pale link.
-
Make the start of the original pale link black. This
eliminates both pale links so there is nothing more to be
done.

Conditions assumed from failure of earlier case conditions: the
pale link is not the root link so the pale link has a sibling.
Then the niece links exist though their end nodes may be null.
Also the far niece is not red.
If the near niece is red then the near niece link should be
rotated.
This does not fix the pale link but it makes the far niece red
so the previous case will apply on the next iteration of the
loop.

Conditions assumed from failure of earlier case conditions:
neither niece is red.
If the parent is red then the colors across the sibling link
should be swapped.
This does not change the number of black node on paths through
the sibling link but it adds a black node to paths through the
pale link.
That fixes the pale link so no more needs to be done.

If none of the preceeding case conditions are true then the
parent, sibling, and niece nodes (if they exist) are all black.
Then the sibling should be made red.
This does not fix the pale link.
Instead it creates a situation where all paths through the
parent link are short by one black node and all paths that are
short by a black node go through the parent link.
Thus we should set the pale link to the parent of the original
pale link and continue the loop.

Section overview text.

Although rebalancing code for red-black trees seems complex, it
does not add much time to handling inserts and deletes.
It can be shown that the amortized rebalancing time is constant.
This means that the worst case average rebalancing
time for a sequence of inserts and deletes is constant.
In return for this you get a worst case O(log n) bound
on the tree height as opposed to O(n) for an unbalanced
tree.
The balancing also improves the average tree height by about
25%.
For trees with ~100 nodes or more this reduces the search time
significantly.
Since a search is involved in both inserts and deletes, the
rebalancing actually reduces the overall average insert and
delete time for moderate to large size trees.