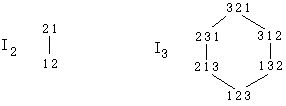1 Smooth Numbers.
Many factoring algorithms require one to find numbers in some range with only small prime divisors. This has lead to the study of such numbers. A number with all prime divisors less than x is called x-smooth. For example, the 10 smooth numbers up to 100 are:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 49, 50, 54, 56, 60, 63, 64, 70, 72, 75, 80, 81, 84, 90, 96, 98, 100.
There are 46 such numbers. This sounds like a lot: almost half of these numbers is 10 smooth. But now they start getting rarer: there are 140 10 smooth numbers up to 1000 fraction: .14 , there are 332 up to 10,000 fraction: .0322 , and 587 up to 100,000 fraction .00587 .
It is known that this fraction is, in general, very regular: if f(n, x) is the fraction of n smooth integers up to n x , then f(n, x) approximately satisfies the differential delay equation
f(n, x) = 1, if x <= 1,
f '(n, x) = - f(n, x-1)/x, if x > 1,
and the approximation gets better as n gets bigger.
Recently, I have gotten interested in numbers that are “smooth” with respect to some set of primes. For example, suppose we have the set of primes 2, 5, 7 , and we want all numbers less than 100 which have only these primes as divisors. The list is:
1, 2, 4, 5, 7, 8, 10, 14, 16, 20, 25, 28, 32, 35, 40, 49, 50, 56, 64, 70, 80, 98, 100.
Now there are only 23 such numbers, and there are only 56 of these numbers up to 1000.
This project would be to investigate properties of numbers which are smooth with respect to a set of primes, or with respect to multiple sets of primes. In particular, it appears that there are functions like f that tell approximately how many such numbers there should be.
2) Carmichael numbers.
It is known that there are infinitely many Carmichael numbers. In fact, if C(x) is the number of Carmichael numbers < x, then it has been proven that C(x) > x2/7 , for all x sufficiently large. It is conjectured that for each e > 0, there is an N for which C(x) > x1- e for all x > N. In particular, there should be an N for which C(N) > sqrt(N). The goal of this project would be to find such an N. (One of the reasons: Many mathematicians are, or were, skeptical of this claim.)
Erdos’s approach: Let M be a highly composite number. For example, we might use M = lcm(1, 2, , n) for some integer n. Let P be the set of primes P = {p : p does not divide M but p - 1 does divide M}.
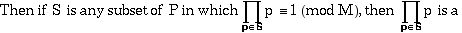Carmichael number. If such products are uniformly distributed among the
reduced residue classes of M (as would be expected , then we should 
Modifications on this approach support the conjecture that C(x) >
x 1-e.3) Find a number which is both a base 2 pseudoprime and a
Fibonacci pseudoprime.
This is a problem of Pomerance, Selfridge and Wagstaff, and carries a cash reward of $620 to the first one discovered!
If p is a prime, then ap = a mod p for every integer a. If n is not prime, but 2 n = 2 mod n, then n is called a base 2 pseudoprime.
If Fn refers to the n’th Fibonacci number, so F0 = 0, F1 = 1, F n = Fn-1 + Fn-2, then it is a theorem that if p is a prime, and p = 2 or 3 mod 5, then F p = -1 mod p. If n is not prime, n = 2 or 3 mod 5, and Fn = -1 mod n, then n is called a Fibonacci pseudoprime.
Thus, the goal of this project would be to find a nonprime number n such that n = 2 or 3 mod 5, 2n = 2 mod n, and Fn = -1 mod n. There are techniques for attempting this, which are modifications of the techniques that work in (2). I already had a student work on this, but there is still lots of stuff to be done. Here is one possible offshoot: we have a very large set of primes P, and a large number M. What we need is to show that for each reduced residue class of M, there is a subset of P with product congruent to that residue class modulo M. For a small example, if M = 25 and P = {2, 3, 7, 11, 13, 17} , then the reduced residue classes of M are 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19, 21, 22, 23, 24. Products of the elements in subsets of P mod 25 are: 2, 3, 7, 11, 13, 17, for one element subsets, 6, 14, 22, 1, 9, 21, 8, 16, 19, 18, 12 for two element subsets, 4, 24, 23 for three element subsets and we don’t need larger subsets. Here, we could do the calculations. What can be said when M and P are too big to actually calculate all products?
4) Stuff related to pi.:
a) Setting up the Bailey, Borwein and Plouffe formula to
calculate n’th hex digit without having calculated
previous digits.
The formula:
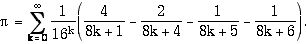
b) Finding similar formulas for pi and other constants.
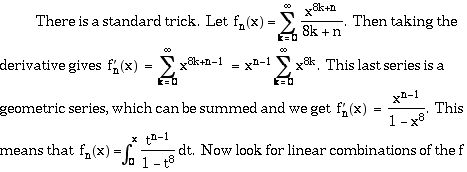
that have nice simplifications. Of course, this trick works for numbers other than 8.
5) Computations related to the average number of prime divisors
and largest prime divisor of a number.
An easy argument based on the above says that the largest prime divisor of a random number n should be about n1-1/e . How good is this estimate? A possible project is to investigate these and other similar questions by doing actual computations of w(n) and for large ranges of n. This can probably all be done in single precision arithmetic.
6) Elliptic curve factoring algorithm.
This algorithm is a variation on Pollard’s p-1 method. In the p-1 method, one takes a large number M with lots of factors (a common choice is M = lcm(1, 2, 3, ... , k) for some suitable k) and calculates gcd (2 M-1, n). By Fermat’s little theorem, this greatest common divisor will be divisible by a prime divisor p of n if p - 1 is a divisor of M.
In the elliptic curve algorithm, we use a similar idea, except that we use the group of an elliptic curve mod p to do our calculations, rather than the group U(p). That is, by Lagrange’s theorem, if G is a group of order m, then for any element a of the group, a m = 1. For the p - 1 method, the group is U(p), which has order p - 1. For every elliptic curve C, and almost every prime p, there is a group E(C, p). Elliptic groups have a nice spread of orders. If a number n has a factor p, and if the order of E(C, p) is a divisor of M, then p can be discovered by attempting to calculate a M in the pseudo group E(C, n), where a is an element of E(C, n).
7) Variations on the Quadratic Sieve.
The quadratic sieve factoring algorithm is an algorithm for factoring a large number N. It involves the following steps:
(1) Select a “Base” of primes to use later on. For each of these primes, p must have the property that N = a2 mod p for some a. That is, N must be a square mod p.
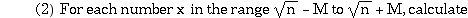f(x) = x2 - n and
use a sieve method to locate those f(x) that factor completely over the
Base found in step 1. Such a factorization of an f(x) is called a relation.
M must be large enough that the number of relations is greater than the
size of the Base.(3) Using basic linear algebra, find several sequences of x such
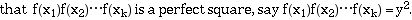
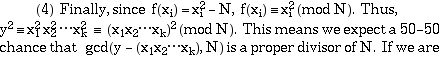unlucky and this gcd is 1 or N, use a different sequence found in step
3. Thus, if we found 10 such sequences in step 3, this would give us 10 chances
to factor N.a) Large prime variation
In this variation of the algorithm described above, in step 2, keep track of those x for which f(x) factors completely over the base OR f(x) factors completely except that one “large” prime factor of f(x) is outside the base. If we found x1 and x2 for which f(x 1) and f(x 2 ) each had the same large prime, then x 1 x2 has that prime squared, and can be added to the list relations. This can cut the size of M needed in step 2. More sophisticated versions of the algorithm allow for two large primes rather than one.
b) Multiple polynomial method
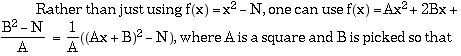B2 = N (mod A).
In this case, the base found in step 1 will still work, and with many choices
of A and B to chose from, we can usually get by with a much smaller M.c) Number field sieve
8) Symmetric chains in partially ordered sets.
Symmetric chain decompositions of B3 and B4 are
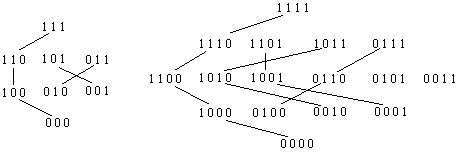
A chain is symmetric if it starts and ends the same distance from the middle of the poset. So, for example, the chain 0100 0110 0111 starts one level below the middle and ends one lever above the middle. A symmetric chain decomposition is a partitioning of the poset so that every element is on some symmetric chain. For B4 above, the elements 0101 and 0011 are each parts of chains with 1 element. We obviously need this if the middle level is larger than any other level. The problem: write and implement an algorithm that searches a partially ordered set for symmetric chains. The sets I have in mind: I n the inversion posets: consists of all permutations of {1, 2, 3, ... , n}. One permutation is just larger than another if it can be obtained from the other by interchanging two adjacent elements, with the left originally smaller than the right. One permutation is larger than another if a sequence of such interchanges can take one to the other.
