ECE 2212
Experiment 3: Frequency Dependent Operational Amplifier Circuits And
Oscillators
Fall 2012
27 September
2012
PURPOSE
To implement the designs of a:
Ø An active analog Low-Pass Filter (LPF)
Ø An active analog High-Pass Filter (HPF)
Ø Wien Bridge Oscillator
Ø Phase Shift Oscillator
PRELAB
Design the Low Pass and High
Pass Filters to meet the indicated specifications. You
should come to the lab with a list of the components you will need to meet the
specifications. For the Low-Pass Filter, the corner frequency is computed from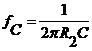 
and the low frequency
voltage gain is given by 
and for the High-Pass
Filter,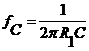 
and the high frequency
voltage gain is given by 
. The derivation of
the corner frequencies follows that of the passive RC filter circuits from
Experiment 1, Problem Sets and the class notes.
Include the derivations in your notebook.
PROCEDURE
Refer to the mA741 data sheet. Observe, again that you are
using the 8-pin DIP. You do not need to include the 10 kW offset voltage potentiometer. All resistors
must be at least 2
kW. Use ± 12 volts for the power supplies. Your
Low Pass, High Pass and Band Pass filter designs should be supported
analytically and by SPICE simulations. Use the library model
for the mA741. Always look at your output waveforms
experimentally to insure you are not clipping.
Explain why you will observe clipping when you use the mA741 while performing a .TRAN simulation and you will not observe
clipping when you use the generic op amp model which consists of only a
voltage-controlled generator.
1.
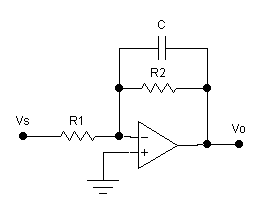
Design
and test an low-pass filter with a low-frequency voltage gain of 20 dB and a 3
dB corner frequency in the range of 3
to 5 kHz. Do not use series and parallel capacitor
combinations or series and parallel resistor combinations . Use standard values that yield a corner frequency and voltage
gain reasonably close to the specifications.
Ø Experimentally verify your design and
simulation results.
Ø For verifying low-pass filter operation,
measure 20 log|A(jf)| and q(jf) and compare
your results with the SPICE .AC simulation over a similar range.
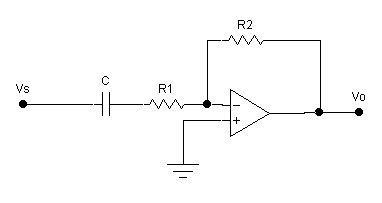
2. Design and
test a high-pass filter with a high-frequency voltage gain of 20 dB and a 3 dB
corner frequency in the range of 100 Hz to 500 Hz. Do not use series and parallel capacitor
combinations or series and parallel resistor combinations. Use standard values that yield a corner frequency and voltage
gain reasonably close to the specifications
Ø Experimentally verify your design and
simulation results.
Ø For verifying high-pass filter operation,
measure 20 log|A(jf)| and q(jf) and compare
your results with the SPICE .AC simulation over a similar range.
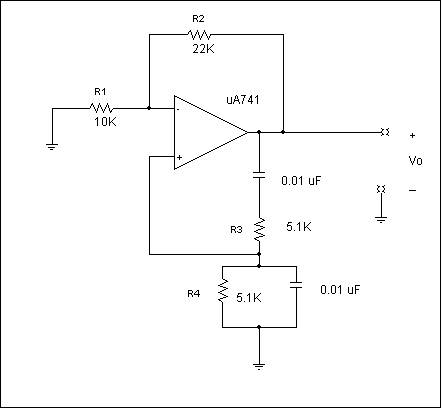
3. Construct the
following circuit which is similar to what is shown in Figure 12.45 on page 755
of the text. At first glance, the
circuits look different but they are the same.
You are generating a signal source, that is an
oscillator. Observe that there is no
external signal generator! Monitor Vo(t) using your oscilloscope. Observe there is no input signal. This is called a Wien Bridge Oscillator. Explain why this is a useful circuit. (Note depending upon the resistor tolerances
and circuit losses, you may have to increase your value of R2 somewhat; perhaps
as high as 33 kΩ). Lead dress has an impact on the circuit
performance. Compare the observed
frequency of operation to the equation, 
and the voltage gain
required setting established by
The SPICE simulation approach is interesting and I will
demonstrate this when we get to lab. In
a real circuit, an oscillator starts through random noise which provides an
initial signal with the correct phase shift to obtain positive feedback . I like to
compare an oscillator starting with the howling noise in a public address
system when the microphone is in the speaker sight range. To
show this in a SPICE simulation, add an initial condition of several volts to
each of the capacitors and then use a .TRAN analysis that extends for several
periods of the expected frequency output.
The signal growth is kind of cool to watch during the simulation.
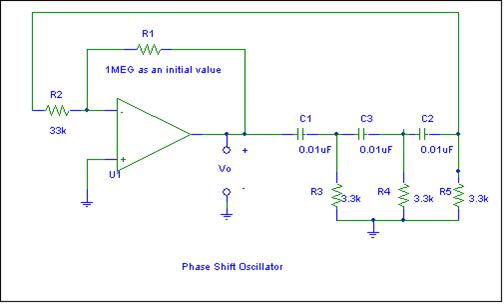
4. Construct the
following circuit similar (but not exactly like) to what is shown in Figures 12.47 and
12.48 on page 756 of the text. Monitor Vo(t) using your oscilloscope. Observe there is no input signal. This is called a Phase Shift Oscillator. Explain why this is a useful circuit. (Note depending upon the resistor tolerances,
you may have to increase your value of R1). Compare the observed frequency of
operation to the
equation, 
and
the voltage gain required setting established by 
. As
with the Wien Bridge oscillator SPICE simulation, add an initial condition of several
volts to each of the capacitors and then use a .TRAN analysis that extends for
several periods of the expected frequency output. Again, it is interesting and fun to watch the
signal growth as a function of time.
As we proceed in our studies of
electronic circuits and devices, you might find the following useful. Also refer to what you learned in ECE 1315
and ECE 2325.
And if
all else fails, blame it on Murphy’s law. An
unabridged version of Murphy’s law Coming Soon. No
engineer should be without it!
