EE 2212
Fall 2014
11 September 2014
Experiment 1: RC
Circuits-Frequency and Time Domain Response Measurements
Note: Experiment
1 Scheduled For Thursday, 11 September.
Report Due Thursday, 18 September, In Lab
LABORATORY NOTEBOOKS AND INFORMATION
Ø Review the Laboratory Information document
on the EE 2212 WEB site including the grading rubric.
Ø I want to emphasize that your report is to
be no more than three additional pages besides the cover page. This will require that you look at your results
with an “engineering eye” to distill and summarize your results.
Ø Every student will keep a patent-style
laboratory notebook. Patent-style
refers to a numbered page bound notebook.
Loose leaf binders are not allowed and would not be legally accepted in
a patent filing. Everything you do in
lab and related to the lab which includes lab preparation, in-lab discussion, prelabs, data, comments during the
lab, etc. are
to be included in the notebook.
Ø The notebook is a stand-alone document from
which a colleague with similar background and experience would be able to
understand and reproduce your results.
This means key diagrams, connection diagrams, design equations,
etc.
Ø If there are errors or problems
encountered in the laboratory, these
are also to be included in your notebook so that a colleague could study the
approach you took to move to a better approach.
Ø No loose sheets of paper are to be used for
data collection.
Ø Date your entries in your notebook. This is a standard practice for IP
(Intellectual Property) in a patent style notebook.
Ø You can tape or staple in graphs, screen
dumps, SPICE plots, etc and/or alternatively, reference locations where data
files, resides should anyone request to see it. (i.e.
flash drives, computer files, etc.)
Ø Your notebook is your key working document
from which you will use
generate high-quality reports.
I encourage you to annotate your results with key statements, comments,
and conclusions as you proceed though the experiments.
Ø I will review your notebooks periodically
through the semester.
Ø If any equipment is not working or if there
are no components in the bins, do not keep it a secret. Please let me know so that I can address the
problem.
Ø Do not put defective components back in the
bins and do not put defective leads and cables back on the cable rack. Give the
defective leads to me and I will bring them to the shop for repairs.
NOW TO THE EXPERIMENT
OBJECTIVES
This laboratory is designed to
be a review of some key EE 2006 concepts and a review of the lab equipment
operation..
Ø Review the operation of the Tektronix TDS 3012B Two-Channel
Color Digital Oscilloscope, Tektronix
AFG 3021C Function Generator, Fluke 8808A DMM, and Impedance Bridge for measuring capacitor
values, and the LAN connected to the oscilloscope, computer, and printer.
Ø There are a number of soft-key nested menus
for you to explore on both the oscilloscope and function generator.
Ø Be able to print Tektronix TDS 3012B screens
to the networked printer on each bench.
Ø Be able to store Tektronix TDS 3012B screens
to your flash drive on the networked computer.
Ø Be able to insert images from SPICE and
Tektronix TDS 3012B screens into document files.
Ø Measure and plot the time and frequency
domain responses of single section RC circuits.
Ø Apply the RC response to illustrate the
concept of a passive element integrator and differentiator in the time domain.
Ø Use SPICE for AC and TRAN simulations to
compare with your analysis and measurements.
PRELAB
Ø You must have a patent-style laboratory notebook
with you. That is a bound notebook (not looseleaf) with numbered pages.
Ø Review the appropriate EE 2006 material
related to first-order time domain system responses and frequency domain
impedance concepts. This will be
reviewed in lab.
Ø
Review SPICE material from EE 2006 so that you will be
able to write and run SPICE programs for each of the circuits for this
lab. SPICE is also available on the
computers in the laboratory and those of you with wireless laptops can also
access the network from
MWAH 391. Print the
waveforms of the inputs and outputs on the same set of axes. You will need to
read the entire experiment to be able to understand what is expected and where
you will need the SPICE graphs. SPICE will be demonstrated in lab. You will
need the following information from your SPICE simulation in order to complete this lab:
· 3 dB BW (bandwidth), tr
(rise time), t (time constant), key amplitudes and times
·
AC
analysis of frequency and phase for the frequency domain
·
TRAN
analysis for the time domain
PROCEDURE
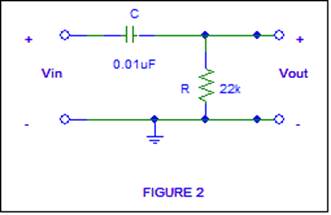
1. Time Domain First Order System Analysis
Construct the following two
circuits on your prototype board. Observe that the circuits are duals of each
other.
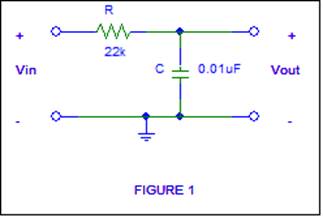
TIME DOMAIN RESPONSE Of Figure 1
Ø Drive Circuit 1 with a 2 volt peak-to-peak square wave and
observe the output. You will need to
adjust the frequency of the square wave such that key attributes of the
waveform are shown for a first-order response.
The 2-volt level is not critical.
The first order response equation is given by:
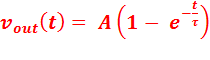 where the time constant
τ = RC. A is the amplitude of vin(t).
where the time constant
τ = RC. A is the amplitude of vin(t).
Ø To
measure the time constant t, determine t63% which is the time required for the
output to reach 63% of its final value during a half-cycle of the input. Does it equal the actual value of the RC
product for your measured values of the resistors and capacitors you are using?
Why or why not? You may need to change
the horizontal time scale and vertical gain of the oscilloscope (and the
amplitude of the input, if needed) to attain this measurement. Save key
waveforms on flash drive. Measure and
record the time constant t.
Ø Also, measure the rise time tr and
record. ( tr
= t90% - t10% = 2.2t).
Finally, compare the theoretical, experimental, and SPICE values of time
constant and rise time. Many of
these measurements can be done by using settings within the oscilloscope “MEASURE” menu. Fill in the following table. This is a good table to include in your lab
report.
|
Parameter |
Calculated |
SPICE |
Measured |
Comments |
|
Rise Time, tr |
|
|
|
|
|
Time Constant, τ |
|
|
|
|
Ø Now change the frequency of the input square wave
from approximately 1 kHz to 30 kHz and adjust your amplitude appropriately to observe
key waveform attributes so that you can observe that this circuit behaves as an
analog passive integrator. That is over
a limited range, ![]()
Ø Now apply a triangular wave to the input of
the circuit. Note input and output waveforms, amplitudes and times. Do these
measurements agree with the values and expected circuit time response you found
using SPICE?
TIME DOMAIN RESPONSE Of Figure 2
Ø Drive Circuit 2 with a 2 volt peak-to-peak square wave
(amplitude is not critical) and observe the output. You will need to adjust the frequency of the
square wave such that key attributes of the waveform are shown for a
first-order response. The first order
response equation is given by:
![]() where the time constant
τ = RC. A is the amplitude of vin(t).
where the time constant
τ = RC. A is the amplitude of vin(t).
Ø To measure the time constant t, determine t37% which is the
time required for the output to reach 37% of A during a half cycle of the
input. Does τ = RC for your measured values of the
resistor and capacitor you are using? Why or why not? You may need to change the horizontal time
scale and vertical gain of the oscilloscope (and the amplitude of the input, if needed)
to attain this measurement. Save key waveforms on flash drive. Measure and record the time constant τ.
Ø Also, measure the fall time tf and record. ( tf = t90% - t10%
= 2.2t). Finally, compare the theoretical,
experimental, and SPICE values of time constant and rise time. Many of these measurements can be done by
using settings within the oscilloscope “MEASURE” menu. Fill in the following table. This is also a good table to include in your
lab report.
Ø
|
Parameter |
Calculated |
SPICE |
Measured |
Comments |
|
Fall Time, tf |
|
|
|
|
|
Time Constant, τ |
|
|
|
|
Ø Now change the frequency of the input square wave from
approximately 1 kHz to 30 kHz and adjust your amplitude appropriately to
observe key waveform attributes so that you can observe that this circuit
behaves as an analog passive differentiator.
That is over a limited range, 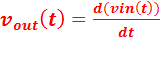 .
.
Ø Now apply a triangular wave to the input of
the circuit. Note input and output waveforms, amplitudes and times. Do these
measurements agree with the values and expected circuit time response you found
using SPICE?
Frequency Domain Response Of Figure 1 (Low-Pass
Filter)
The circuit in Figure 1 is also
a basic single-pole analog passive low-pass filter (LPF). This LPF function can
be observed by applying a constant-amplitude
(i.e. 2 volt peak-to-peak amplitude input sinusoid
and varying the frequency from 50 Hz to > 10 kHz.
Ø Measure and record the
"low-frequency" (f = 50 Hz) gain and phase shift. Use the magnitude
of this gain to measure accurately the – 3 dB corner frequency of the filter,
and the phase shift. (Note that –3 dB
corresponds to 70.7% of the low-frequency gain). Again, you can obtain phase directly from the
“MEASURE” menu and visually verify by looking at the waveforms. Compare these measurements with theoretical
and PSPICE values. Many of these measurements can be done by using settings
within the oscilloscope
“MEASURE” menu. Measure
and plot the gain and phase shift at several frequencies out to >10 kHz. Is
the high-frequency gain roll-off about –6dB/octave (-20dB/decade) as the
frequency is increased? Plot the data as
you change the frequency to ascertain the detail you need.
Ø Finally, using SPICE, show a db plot of 20 log |A(jf)| and a phase plot of q (jf) (voltage
gain and phase as a function of frequency) of the circuit of Figure 1 Vary the
frequency from 50 Hz to >10 kHz. Select data points that show the key
features of the curves. This is a good table to include in your lab
report.
Ø
|
Parameter |
Calculated |
SPICE |
Measured |
Comments |
|
Low Frequency Gain |
|
|
|
|
|
Low Frequency Phase |
|
|
|
|
|
3 dB Frequency |
|
|
|
|
|
Gain at 3 dB Frequency |
|
|
|
|
|
Phase at 3 dB Frequency |
|
|
|
|
FREQUENCY DOMAIN RESPONSE Of Figure 2 (High
Pass Filter)
The circuit in Figure 2 is also
a basic single-pole passive high-pass filter. To see this, observe the
amplitude of the output as the frequency is varied from >10 kHz down to 50 Hz. You will
need to use a 2 volt peak-to-peak constant-amplitude input sinusoid.
Ø Measure the high-frequency (f >10 kHz)
gain and phase shift. Use the magnitude of this gain to measure fc
and the phase shift there. Compare these measurements with your PSPICE values.
Ø Measure the gain and the phase shift of the
filter at low frequencies. Is the low-frequency gain roll-off about -6dB/octave
as the frequency is decreased? Again,
Many of these measurements can be done by using settings within the oscilloscope “MEASURE”
menu.
Ø Finally, using SPICE, show a plot of 20 log
|A(jf)| and q(jf) of the
circuit of Figure 2. Vary the frequency from 50 Hz to 10 kHz. Select data
points that show the key features of the curves. Again, plot the data as you proceed and
change the frequency. This is a good table to include in your lab report.
Ø
|
Parameter |
Calculated |
SPICE |
Measured |
Comments |
|
High Frequency Gain |
|
|
|
|
|
High Frequency Phase |
|
|
|
|
|
3 dB Frequency |
|
|
|
|
|
Gain at 3 dB Frequency |
|
|
|
|
|
Phase at 3 dB Frequency |
|
|
|
|
Now for a little technically
appropriate humor.


