EE 2212

Spring 2013

31 January 2013

Experiment 1: RC Circuits-Frequency and Time Domain Response Measurements

Note: Experiment 1 report due Thursday, 7 February in lab.

LABORATORY NOTEBOOKS AND INFORMATION

Ø LabInfo.docx includes overall requirements and the laboratory report grading rubric

Ø Every student will keep a patent-style laboratory notebook. Patent-style refers to a numbered page bound notebook. Loose leaf binders are not allowed. Everything you do in lab and related to the lab which includes lab preparation, in-lab discussion, prelabs, data, comments during the lab, etc. are to be included in the notebook.

Ø The notebook is a stand-alone document from which a colleague would be able to understand and reproduce your results. This means key diagrams, connection diagrams, design equations, etc.

Ø If there are errors or problems in the lab, these are also to be included in your notebook so that a colleague could study the approach you took to move to a better approach.

Ø No loose sheets of paper are to be used for data collection.

Ø Date your entries.

Ø You can tape or staple in graphs, screen dumps, SPICE plots, etc and/or alternatively, reference locations where data files, Flash drives, etc. where such lab data resides should anyone request to see it.

Ø Your notebook is your key working document from which you can generate high-quality reports. I encourage you to annotate your results with key statements, comments, and conclusions as you proceed though the experiments.

Ø I will review your notebooks periodically through the semester.

Ø If any equipment is not working or if there are no components in the bins, do not keep it a secret. Please let me know so that I can address the problem.

NOW TO THE EXPERIMENT

OBJECTIVES

This laboratory is designed to be a review of some key EE 2006 concepts and a review of the lab equipment operation..

Ø Review the operation of the Tektronix TDS 3012B Two-Channel Color Digital Oscilloscope, Agilent (Hewlett Packard) 33120A Function Generator, Agilent 3631A Power Supply, Impedance Bridge for measuring capacitor values, and the LAN to from the oscilloscope to the computer and printer.

Ø Be able to print Tektronix TDS 3012B screens to the networked printer on each bench.

Ø Be able to store Tektronix TDS 3012B screens to your flash drive on the networked computer.

Ø Be able to insert images from SPICE and Tektronix TDS 3012B screens into document files.

Ø Measure and plot the time and frequency domain responses of single section RC circuits.

Ø Apply the RC response to illustrate the concept of a passive element integrator and differentiator in the time domain.

Ø Use SPICE for .AC and .TRAN simulations to compare with your analysis and measurements.

PRELAB

Ø You must have a patent-style laboratory notebook with you. That is a bound notebook (not looseleaf) with numbered pages.

Ø Review the appropriate EE 2006 material related to first-order time domain system responses and frequency domain impedance concepts.

Ø Review EE 2006 topics related to first-order systems time and frequency domain analysis.

Ø Review SPICE material from EE 2006 so that you will be able to write and run SPICE programs for each of the circuits for this lab. SPICE is also available on the computers in the laboratory and those of you with wireless laptops can also access the network from 391 MWAH. Print the waveforms of the inputs and outputs on the same set of axes. You will need to read the entire experiment to be able to understand what is expected and where you will need the SPICE graphs. You will need the following information from your SPICE simulation in order to complete this lab:

· 3 dB BW (bandwidth), t_r (rise time)_, t (time constant), key amplitudes and times

· .AC analysis of frequency and phase for the frequency domain

· .TRAN analysis for the time domain

PROCEDURE

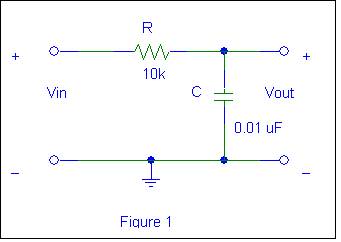
1. Circuit 1 (Time Domain and Frequency Domain Response)

TIME DOMAIN RESPONSE (Integrator)

Ø Construct the circuit in Figure 1.

Ø Drive it with a 2 volt peak-to-peak square wave (amplitude is not critical) and observe the output. You will need to adjust the frequency of the square wave such that key attributes of the waveform are shown. To measure the time constant t, determine t_63% which is the time required for the output to reach 63% of its final value during a half-cycle of the input. Does it equal the actual value of the RC product for your measured values of the resistors and capacitors you are using? Why or why not? You may need to vary the horizontal time scale and vertical gain of the oscilloscope (and the amplitude of the input, if needed) to attain this measurement. Save key waveforms on flash drive. Measure and record the time constant t.

Ø Also, measure the rise time t_r and record. ( t_r = t_90% - t_10% = 2.2t). Finally, compare the theoretical, experimental, and SPICE values of time constant and rise time.  Many of these measurements can be done by using settings within the oscilloscope “MEASURE” menu.

Ø Drive the circuit in Figure 1 with a square wave approximately in the 2 kHz to 30 kHz range. Adjust your amplitude appropriately to observe key waveform attributes. Observe the input and output waveforms and measure key amplitudes and times. Compare the input and output waveforms from your SPICE program to that of the oscilloscope waveforms. Are they the same? Why does the output have the shape that you see? Again, exercise the automated settings within the “MEASURE” menu to support your results. Compare the automated measurements with visual observation of the key waveform attributes.

Ø Now apply a triangular wave to the input of the circuit. Note input and output waveforms, amplitudes and times. Do these measurements agree with the values and expected circuit time response you found using SPICE?

Ø Reapply the square wave and decrease the frequency until the output shape deviates appreciably from an integrator response. Why does the output no longer appear linear?

Ø Fill in the following table:

Parameter	Calculated	SPICE	Measured	Comments
Rise Time
Time Constant

Frequency Domain Response (Low-Pass Filter)

The circuit in Figure 1 is also a basic single-pole analog passive low-pass filter (LPF). This LPF function can be observed by applying a constant-amplitude (i.e. 2 volt peak-to-peak amplitude input sinusoid and varying the frequency from 100 Hz to > 30 kHz.

Ø Measure and record the "low-frequency" (f = 100 Hz) gain and phase shift. Use the magnitude of this gain to measure accurately the – dB corner frequency of the filter, and the phase shift. (Note that –3 dB corresponds to 70.7% of the low-frequency gain). Again, you can obtain phase directly from the “MEASURE” menu and visually verify by looking at the waveforms. Compare these measurements with theoretical and PSPICE values. Many of these measurements can be done by using settings within the oscilloscope “MEASURE” menu. Measure and plot the gain and phase shift at several frequencies out to >30 kHz. Is the high-frequency gain roll-off about –6dB/octave (-20dB/decade) as the frequency is increased? Plot the data as you change the frequency to ascertain the detail you need.

Ø Finally, using SPICE, show a db plot of 20 log |A(jf)| and a phase plot of q (jf) (voltage gain and phase as a function of frequency) of the circuit of Figure 1 Vary the frequency from 100 Hz to >30kHz. Select data points that show the key features of the curves. 

Parameter	Calculated	SPICE	Measured	Comments
Low Frequency Gain
Low Frequency Phase
3 dB Frequency
Gain at 3 dB Frequency
Phase at 3 dB Frequency

Ø

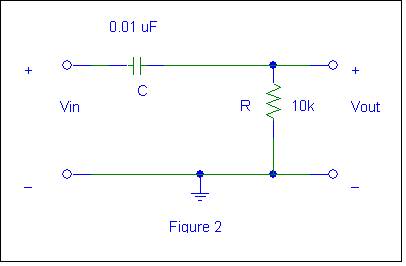
2. Circuit 2 (Time Domain and Frequency Domain Response)

TIME DOMAIN RESPONSE (Differentiator)

Ø Construct the circuit of Figure 2. Drive it with a 2 volt peak-to-peak, square wave and observe the output. You will need to adjust the frequency of the square wave such that key attributes of the waveform are shown. Does it match the SPICE program you wrote? Can you explain the shape of the output waveform? Give theoretical justification.

Ø Measure t _37% (the time required for the output to fall to 37% of its peak value during the appropriate half-cycle of the input). Does it equal the actual value of the time constant of the circuit? Also measure the fall time t _f = t _10% - t _90% = 2.2t.

Ø Now apply a 30 Hz triangular wave to the input of the circuit. Note the key amplitudes and times. Does it match your SPICE graphs for this circuit? You will have to increase the vertical sensitivity of the scope and/or the input amplitude to observe the output.

Parameter	Calculated	SPICE	Measured	Comments
Rise Time
Time Constant

FREQUENCY DOMAIN RESPONSE

The circuit in Figure 2 is also a basic single-pole passive high-pass filter. To see this, observe the amplitude of the output as the frequency is varied from >30 kHz down to 100 Hz. You will need to use a 2 volt peak-to-peak constant-amplitude input sinusoid.

Ø Measure the high-frequency (f >30 kHz) gain and phase shift. Use the magnitude of this gain to measure f_c and the phase shift there. Compare these measurements with your PSPICE values.

Ø Measure the gain and the phase shift of the filter at low frequencies. Is the low-frequency gain roll-off about -6dB/octave as the frequency is decreased? Again, Many of these measurements can be done by using settings within the oscilloscope “MEASURE” menu.

Ø Finally, using SPICE, show a plot of 20 log |A(jf)| and q(jf) of the circuit of Figure 2. Vary the frequency from 30 Hz to 30 kHz. Select data points that show the key features of the curves. Again, plot the data as you proceed and change the frequency.

Parameter	Calculated	SPICE	Measured	Comments
High Frequency Gain
High Frequency Phase
3 dB Frequency
Gain at 3 dB Frequency
Phase at 3 dB Frequency

Ø

Now for a little technically appropriate humor.