EE 2212

Spring 2017

2 February 2017

Experiment 3: Additional Operational Amplifier Circuits

LAB SCHEDULING:

Ø Use lab time, 2 February, to complete Experiment 2. Some of you may have already completed Experiment 2.

Ø The Experiment 2 Lab Report is due on Thursday, 9 February.

Ø Start Experiment 3 and realize that you will have additional time on 9 February to complete Experiment 3. The Experiment 3 Lab Report is due on Thursday, 16 February.

Ø Experiment 2 will be evaluated using the 20-Point rubric. Note that the cover page plus three additional pages limit must be observed.

Ø Experiment 3 will be evaluated using the 40-Point rubric. Note that the cover page plus six additional pages limit must be observed.

Ø FYI. Experiment 4 on 16 February will be on diodes and applications

Purpose

To simulate and implement the designs of:

Ø An active analog Low-Pass Filter (LPF)

Ø An active analog High-Pass Filter (HPF)

Ø An active Band-Pass Filter (BPF)

Ø A Wien Bridge Oscillator

Ø A Phase Shift Oscillator

GENERAL COMMENT

Run SPICE frequency domain simulations with a VAC generator programs for the LPF, HPF, and BPF. Use the μA741 model in the eval.slb library. You will need the following information from your SPICE program in order to complete this lab:

Ø AC analysis including amplitude as a function of frequency from around 10 Hz to at least 10 kHz.

Ø Time domain analysis is not required.

PRELAB

Use your design for the inverting operation amplifier with a voltage gain of 14dB from Experiment 2, Figure 1.

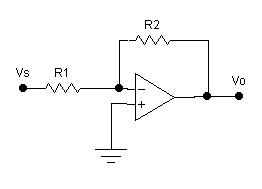
Figure 1

Design the Low Pass and High Pass Filters to meet the indicated specifications. You should come to the lab with a list of the components you will need to meet the specifications. For the Low-Pass Filter, the corner frequency is computed from 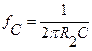and the low frequency voltage gain is given by and for

the High-Pass Filter, 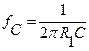and the high frequency voltage gain is given by . The derivation of the corner frequencies follows that of the passive RC filter circuits from Experiment 1. We will also discuss more at the beginning of the lab period. Include the derivations in your notebook.

PROCEDURE

Refer to the mA741 data sheet. Observe, again that you are using the 8-pin DIP. Do not include the 10 kW offset voltage potentiometer. All resistors must be at least 2 kW. Use ± 12 volts for the power supplies. Your Low Pass and High Pass designs should be supported analytically and by SPICE simulations. Use the library model for the mA741. Adjust your input levels to avoid clipping.

1. Design and test an low-pass filter with a low-frequency voltage gain of 14 dB and a 3 dB corner frequency in the range of 2 to 4 kHz, Figure 2. Do not use series and parallel capacitor combinations or series and parallel resistor combinations . Use standard values that yield a corner frequency and voltage gain reasonably close to the specifications.

Ø Experimentally verify your design and simulation results.

Ø For verifying low-pass filter operation, measure 20 log|A(jf)| and compare your results with the SPICE AC simulation over a similar range.

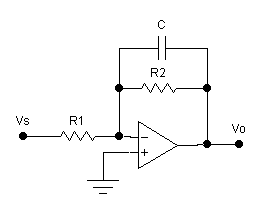
Figure 2 Low Pass Filter

2. Design and test a high-pass filter, Figure 3 with a high-frequency voltage gain of 14 dB and a 3 dB corner frequency in the range of 50 Hz to 200 Hz. Do not use series and parallel capacitor combinations or series and parallel resistor combinations. Use standard values that yield a corner frequency and voltage gain reasonably close to the specifications

Ø Experimentally verify your design and simulation results.

Ø For verifying high-pass filter operation, measure 20 log|A(jf)| and compare your results with the SPICE AC simulation over a similar range.

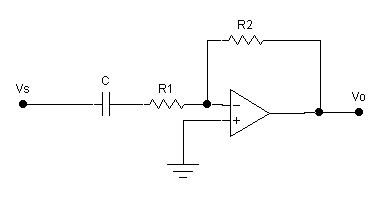
Figure 3 High Pass Filter

3. Band Pass Filter

Ø Now cascade the output of the HPF with the LPF and note the band pass characteristic. Measure 20 log|A(jf)| and compare your results with the SPICE AC simulation over a similar range.

Figure 4 Band Pass Filter

3. Wien-Bridge Oscillator

So far, all of the circuits we have studied employ negative feedback. The following circuit employs positive feedback; and as mentioned in class, an audio example of positive feedback is the “howl” observed when the microphone and speaker are not placed well in an auditorium and you have constructive (additive) signals. Construct the following circuit which is similar to what is shown in Figure 12.43 on page 741 of the text. At first glance, the circuits look different but they are the same. You are generating a signal source, that is you are demonstrating the operation of an oscillator. Observe that there is no external signal generator!!!! Monitor v_o(t) using your oscilloscope. Observe there is no input signal. This is called a Wien Bridge Oscillator. Explain why this is a useful circuit. (Note depending upon the resistor tolerances and circuit losses, you may have to increase your value of R2 somewhat; perhaps as high as 33 kΩ). Lead dress has an impact on the circuit performance. Compare the observed frequency of operation to the equation, and the voltage gain required setting established by.

The SPICE simulation approach is interesting and I will demonstrate this when your group reaches that part of the lab. In a real circuit, an oscillator starts through random noise which provides an initial signal with the correct phase shift to obtain positive feedback . To show this in a SPICE simulation, add an initial condition of several tenths of a volt to each of the capacitors as an initial condition and then use a transient analysis that extends for several periods of the expected frequency output. The exponential signal growth is kind of cool (at least I think so) to watch during the simulation.

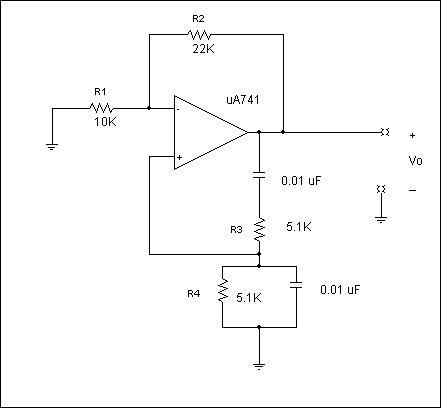
Wien Bridge Oscillator

4. Phase-Shift Oscillator

Construct the following circuit similar (but not exactly like) to what is shown in Figure 12.45 on page 742 of the text. Monitor Vo using your oscilloscope. Observe there is no input signal. This is called a Phase Shift Oscillator. Explain why this is a useful circuit. (Note depending upon the resistor tolerances, you may have to increase your value of R1 or reduce the value of R2 to increase the gain). Compare the observed frequency of operation to the equation, and the voltage gain required setting established by . As with the Wien Bridge oscillator SPICE simulation, add an initial condition of several tenths of volts to each of the capacitors and then use a transient analysis that extends for several periods of the expected frequency output. Again, it is interesting and fun to watch the signal growth as a function of time.

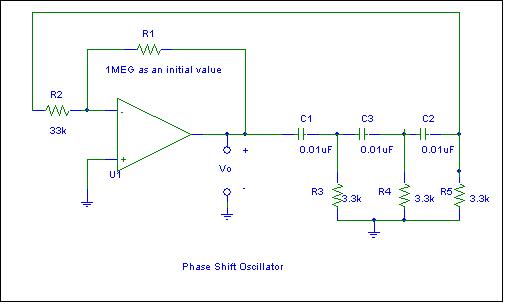
Phase-Shift Oscillator

Do you believe this explanation or the one claiming the WEB originated as a spin-off of a U.S. Department of Defense ARPANET project?

Time to start thinking about out of EE technical electives registration for next semester.

Also UROP