EE 4611
PROBLEM SET 3
S. G. Burns
Due: Wednesday, 2 March 2016
Some mathematical warmup.
1. Show
analytically that 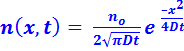 is a solution for
is a solution for ![]() and also show that
and also show that ![]() is also a solution Use the closed form integrals in the class
WEB notes. Do not use MATLAB or
MATHEMATICA. You will have to use the
chain rule for the first equation.
is also a solution Use the closed form integrals in the class
WEB notes. Do not use MATLAB or
MATHEMATICA. You will have to use the
chain rule for the first equation.
The following problems require using the data and
curves (not in the text) but embedded in the class notes PowerPoints related to
semiconductor device design diffusion and oxidation. Also recall the erfc
and Gaussian graphs. The semiconductor device processis
in the overview is in the Prologue and elaborated in a PowerPoint.
2. Assume
that an infinite source profile of boron doping can be approximated by an
exponential of the form![]() . Assume the n-type substrate is doped at ND
= 1017 cm-3.
. Assume the n-type substrate is doped at ND
= 1017 cm-3.
(a) Sketch the diffusion profile
(b) Compute the junction depth in μm.
(c )
Compute a value for the dose, Qo, with
correct units. Although you can use
MATLAB or MATHEMATICA for the integration, the exponential function closed form
by-hand method is probably much quicker.
Whichever you use, show the problem graphical set up.
3. Similar to Problem 2 and extracted partially
from an old quiz. Assume a linear
donor doping profile defined by ![]() as sketched. The substrate
is doped at NA = 1 x 1017cm-3.
as sketched. The substrate
is doped at NA = 1 x 1017cm-3.

(a)
Compute a value for the
junction depth, xj.
(b)
What is the resultant dose, Qo? [You
can make your algebraic life easier by utilizing the linear
nature of the doping profile!]
(c) This predeposition step is now capped and we proceed with a
limited source diffusion for time t1
and temperature T1. During
the time, t1, used for this finite (limited source) drive diffusion,
the surface concentration will (INCREASE, REMAIN
THE SAME, DECREASE), the junction depth, xj,
will (INCREASE, REMAIN THE SAME, DECREASE), and the dose, Qo will
(INCREASE, REMAIN THE SAME, DECREASE).
Circle your choices.
(d)
Suppose the finite (limited)
source diffusion in Part (c) was done at temperature T2, where T2>
T1 and the time remains the same. Comparing to the results from Part (c), the
surface concentration would be (LOWER, ABOUT THE SAME), the junction depth, xj, would be (DEEPER, ABOUT THE SAME, NOT AS
DEEP), and the dose, Qo would be (LARGER, ABOUT THE SAME, SMALLER) Circle your choices.
4. Using
graphs from class notes, answer the following for oxidations:
(a) How
long to grow a 200Å
SiO2 MOSFET gate dielectric at 1000°C. For this, use assume a dry oxidation. Discuss several reasons why this dry oxidation is
preferable to a wet oxidation.
(b) How long to grow a 0.3 μm SiO2 masking layer at
1000°C. For this, assume using a wet oxidation. Discuss several reasons why this wet oxidation is preferable to a dry
oxidation.
5. Assume
a p-doped substrate where NA = 5 x 1015 cm-3
. From an infinite As source ND
= 1 x 1019 cm-3, compute the junction depth, xj, for one hour and a two hour diffusion at
1100°C.
6. Compare
the impurity concentration at 1μm with that of the surface concentration
for a 1 hour and 2 hour diffusion of boron into an n-type substrate at
1100°C To have some consistency in your
solutions, use D=3.5 x 10-13 cm2/sec
7. Refer
to the information about ion implantation
How many
ions Dose, Q) are required to obtain a uniform doping profile of ND
= 2 x 1017 cm-3 to a depth of 1μm? How long will it take to ion implant a 12
inch (300 mm) diameter wafer assuming a beam current of 200 μA?
Assume singly ionized ions.