Other Changes Required for Three-Pile Nim

• A:
  • remove-coins-from-pile
  • display-game-state
  • total-size
  • computer-move

  Converting to three-pile Nim is an assignment exercise.

The Chocolate Bar Game and Two-Pile Nim Are Equivalent

Q: The length and width of the chocolate bar are equivalent to what?

• A: The number of coins in the two piles

  Q: Breaking the bar along a vertical or horizontal score (and eating the part without the poisoned section) is equivalent to what?

• A: Removing one or more coins from a pile.

  Q: Breaking off the last edible piece (and eating it) is equivalent to what?

• A: Taking the last coin(s) on the table.

  Q: What is a winning strategy for two-pile Nim?

• A: Always leave your opponent with two piles of equal numbers of coins.

  Therefore, if a player plays first, and the initial state does not have equal-size piles, he or she can force a win.

     (define make-game-state
       (lambda (i j) (+ (* 10 i) j)))

     (define size-of-pile
       (lambda (game-state pile-number)
         (if (= pile-number 1)
             (quotient game-state 10)
             (remainder game-state 10))))

Q: What is the order of growth of size-of-pile?

• A: Θ(1) — Constant

• A: 9

  Q: How might we represent larger piles, as in:

  ?

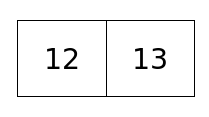•      (define make-game-state
         (lambda (i j) (+ (* 100 i) j)))
  
       (define size-of-pile
         (lambda (game-state pile-number)
           (if (= pile-number 1)
               (quotient game-state 100)
               (remainder game-state 100))))
  
  	 

  This data representation method puts an artificial restriction on the size of piles.

  While this is acceptable for 2-pile Nim, other data types should not be subject to such a restriction.

   (remove-coins-from-pile game-state n p) ; given a state, returns a new
                                           ; state with n fewer coins in pile p
      

• A:

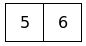  To remove a number of coins n from pile p:

  • Determine if p is 1 or 2
  • Determine the size of pile p (use selector),
  • Create a new game state with n coins removed from pile p (use constructor).

       (define remove-coins-from-pile
         (lambda (game-state n p)
            ... ??? ...
           ))
        

•      (define remove-coins-from-pile
         (lambda (game-state n p)
           (if (= p 1)
               (make-game-state
                 (- (size-of-pile game-state 1) n)
                 (size-of-pile game-state 2))
               (make-game-state
                 (size-of-pile game-state 1)
                 (- (size-of-pile game-state 2) n)))))
        

	  (play-with-turns (make-game-state 5 8) 'humman)
      

• A: If all cond tests fail, the behavior is unspecified.

  play-with-turns should do error handling:

  (define play-with-turns
    (lambda (game-state player)
      (cond 
        ((over? game-state) (announce-winner player))
        ((equal? player 'human) 
         (play-with-turns (human-move game-state) 'computer))
        ((equal? player 'computer) 
         (play-with-turns (computer-move game-state) 'human))
        (else (error "player wasn't human or computer:" player)))))
  

     (play-with-turns (make-game-state 5 8) 'human)
      

     (play-with-turns (make-game-state 5 8) human)   ?
      

• A: Error message: reference to undefined identifier: human

  The quote's function is to prevent evaluation of the next expression.

  A quote before a name causes the name itself to be used, not what it is a name of.

       > (define x 13)
       > x  ⇒ ???
  

• A: 13

       > 'x  ⇒ ???
  

• A: x

       > 'human  ⇒ ???
  

• A: human

       > (define x 'y)
       > (define z x)
       > z ⇒ ???
  

• A: y

• The constructor for the ADT Game State:

     (make-game-state n m) ; returns a state with n coins in
                           ; first pile and m coins in second
  

• A selector for the ADT Game State:

     (size-of-pile game-state p) ; returns number of coins in
                                 ; p-th pile of game-state
  

• Q: (size-of-pile (make-game-state 5 8) 2)= ???
• A: 8

Advantages:

• Programmer is freed from machine details, so he/she can concentrate on the problem domain.
• Programs that use the data can be developed independently of the programs that represent the data.
• Changes to the data representation do not require changes to the programs that use the data.

• Abstraction as non-concreteness:
  • Numbers (abstract) vs. numerals (concrete)
  • Sets (abstract) vs. elements (sometimes concrete)
  • Procedures (abstract) vs. running programs, or processes (concrete)
• Abstraction as universality:
  • An abstraction is that which is shared by individual instances.
  • For example, justice, as an abstraction, is that which is shared by all just acts.
• Abstraction as generality:
  • Distinguishing the general from the particular in the world of ideas.
  • We can have a general idea of water apart from specific ideas of water, e.g. Lake Superior, or my dripping faucet.
  • In chapter 5, we used higher-order procedures to abstract general procedures from more specific ones.
• In all characterizations, abstraction is the process of eliminating specificity by ignoring certain details and features.