In chapter 13 we saw how modifying data using
mutators required the
concept of
state.
We introduced the notion of a Scheme
vector to control the
changing state of
stacks and
queues.
In this chapter we look at the state of a computer system in general by
asking more specifically:
- Q: How is a computer able to carry out
procedurally-specified computational processes?
- A: By continually changing the state of its memory through the
execution of program instructions.
This chapter will provide an introduction to
computer
architecture and
assembly language programming.
Computer architecture is a
structural and
functional view
of computers.
- Structural: Describes components of a system relevant to the
execution of a program
- Functional: Gives operational understanding of the system
by showing inputs and outputs of components
Computer architecture is
not the physical structure of a
computer at the circuit level (like the layout of a chip or
motherboard).
The
core of a computer refers to its
processor
and
memory, omitting input and output devices like the keyboard,
mouse, monitor, and disk drive.
- Processor: Executes program instructions and uses memory
to store and retrieve values as needed.
- Memory: A collection of locations in which values can be
stored and changed.
To access data values, the processor sends the memory unit the
address
of a memory location.
We will describe the architecture of SLIM (Super-Lean Instruction Machine).
- Not a real machine but representative of modern computers.
- Since it is not real, it is simplified.
- We will run it using an emulator written in Java.
- Variations on the SLIM architecture:
- Shared-memory multiprocessor systems (duo-core, quad-core,
etc)
- DMA: Direct Memory Access, in which input
to and output from memory can bypass the
processor
SLIM is a
stored program computer. In such a computer:
- The computer's behavior consists of
executing a list of instructions, called
a program
- The computer's abilities are determined
by its instruction set
- When you turn it on ("boot it up"), an
initial program called an operating
system is run which makes it easy to
run other programs
- Instructions perform operations like:
- Reading from the keyboard
- Storing a value in memory
- Adding the values of two memory
locations and storing the result in a
third, etc.
Recall the role of memory within the computer's core:

- Conceptually, computer memory is a long sequence of "slots" (or
"boxes") that are the individual memory locations.
- In order to allow the processor to uniquely specify each location, the
slots are sequentially numbered starting at 0.
- The number corresponding to a given slot is called its address.
Recall the role of the processor within the computer's core:

- Keep track of what is to be done next
(control unit)
- Store frequently used and critical values
in 32 high speed locations (registers)
- Do the actual operations, such as
addition (arithmetic logic unit or ALU)
Recall the role of the registers in the processor:
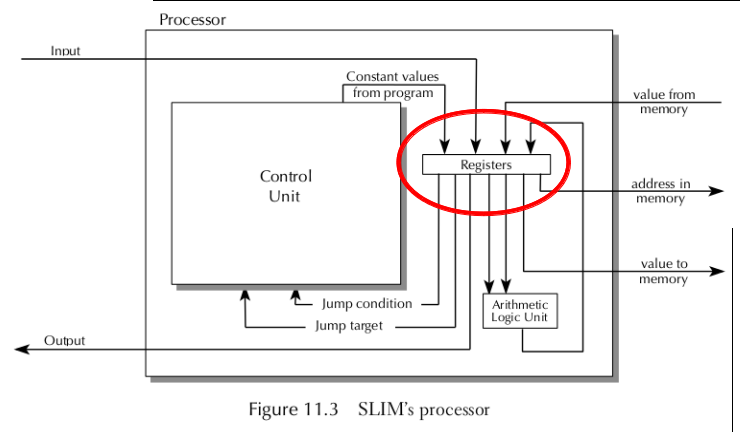
Registers, like memory, can hold data, but:
- They are faster
- They are part of the processor
- There are far fewer registers than memory locations
The SLIM architecture has 32 registers, referred to by number:

- All values get to memory via registers
- All values are retrieved from memory
into registers
- All operations performed by the ALU get
their operands from registers
- All operations performed by the ALU
store results in registers
- There are other processor data paths which:
- Tell the ALU which instruction to do
- Tell the register set which register to
access
- Tell both registers and memory whether to
store or retrieve
Recall the role of the arithmetic logic unit in the processor:

The ALU can perform:
- Arithmetic operations that produce numbers
- Comparison operations that produce the truth values true (1)
and false (0)
| Arithmetic Operations | Comparison
Operations |
|---|
| Addition | = |
| Subtraction | <> |
| Multiplication | < |
| Division | > |
| Quotient | <= |
| Remainder | >= |
- All stored-program architectures store
program instructions in memory of some kind.
- Some architectures store the program in a
reserved area of data memory.
- Other architectures store the program in a
separate instruction memory in the Control
Unit (the "Harvard" architecture).
- SLIM uses the Harvard architecture
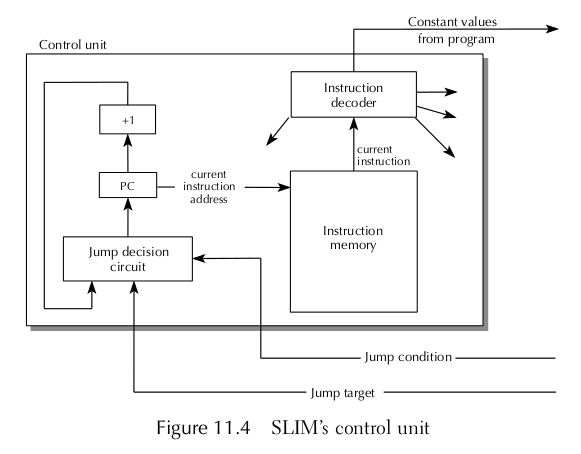
Recall the role of the control unit in the processor:

- At any time, one instruction is designated
the current instruction
- The current instruction resides in
instruction memory and therefore has an
address
- The address of the current instruction is
contained in a special location called the
program counter (PC)
- When the execution of an instruction is
complete, the PC must be updated to contain
the address of the next instruction
- Often, the next instruction is just the one
in the next memory location in instruction
memory. Its address can be calculated by
adding 1 to the address in PC
- Sometimes, the next instruction is not next
in instruction memory:

- Whether or not to perform the instruction at
PC + 1 is computed by circuitry that does
jump decisions
- The decision is based on a jump condition,
specified by the program
- If the instruction at PC + 1 is not to be
performed, the address of the instruction
that is to be performed is retrieved from a
register (the jump target)
Instructions, being patterns of bits, must be
decoded before
they can be carried out.
Decoding circuitry figures out:
- What the operation is (add, sub, ...)
- What the operands are (registers, constants)
Once the instruction is decoded, the control unit sends signals:
- To the operand registers to send their
contents to the ALU
- To the ALU to perform the indicated
operation
SLIM instructions have two notations:
- Machine Language (zeros and ones), for processors
- Assembly Language, for humans
Assembly language instructions are translated into machine language
instructions by programs called
assemblers.
This section describes the SLIM
assembly language.
add 17, 2, 5
means:
"Add the contents of registers 2 and 5 and
store the sum into register 17."

The general form of all arithmetic instructions is:
opcode destreg, sourcereg1, sourcereg2
where:
- destreg is a destination register
number
- the sourceregi are source
register numbers
Other operations will have these kinds of operands:
- addressreg: specify the number of a register that
holds a memory address
- const: specify a constant value
Arithmetic instruction opcodes fall into two groups:
| Operations | Comparisons |
|---|
| add | seq (set equal) |
| sub | sne (set not equal) |
| mul | slt (set less than) |
| div | sgt (set greater than) |
| quo | sle (set less or equal) |
| rem | sge (set greater or equal) |
Arithmetic comparison instructions compare values in the source
registers and set the destination register to
1 (
true)
or
0 (
false) depending on the result of the comparison.
Example. Suppose:
- Register 5 contains 315
- Register 6 contains -17
Then the instruction
slt 4, 6, 5
will compare the contents of register 6 to
the contents of register 5 to determine if
the first is less than the second.
Since it is, then register 4 will be set to
1 (true).
If the instruction were
slt 4, 5, 6
then register 4 will be set to 0 (false).
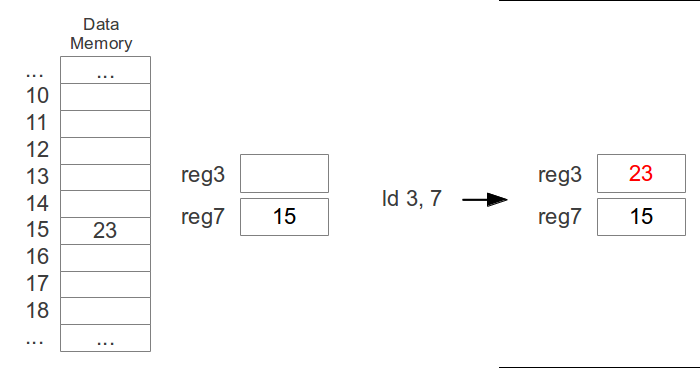
There are two ways of moving values between registers and memory:
- Loading into a register from a memory location:
ld destreg, addressreg
- Storing from a register to a memory location:
st sourcereg, addressreg
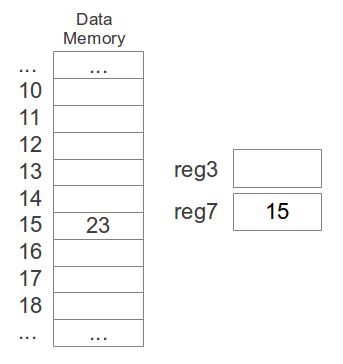
ld 3, 7
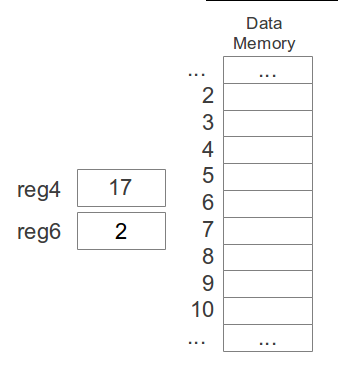
st 4, 6
There are two input/output operations available in SLIM:
- Reading a value from standard input (the keyboard) into a
register:
read destreg
- Writing a value from a register to standard output (the
display):
write sourcereg
Example:
read 1 ; reads a value, say 314, typed at the keyboard into register 1
write 1 ; writes the value in register 1 to the display
These instructions are able to read or write numeric values, but real
machines would only have instructions for reading or writing individual
characters (e.g. '3', '1', '4', etc.).
Another way of getting values into registers is through program
constants.
SLIM uses a
load immediate opcode for this:
li destreg, const
Example:

Suppose SLIM executes the following instructions:
li 1, 314
write 1
The machine would display 314 because it loads that value into register
1 and then writes out the contents of register 1 to the display.
But nothing would stop the machine from going to the third location in
instruction memory and attempting to execute any code contained there.
To halt the machine, use the
halt instruction:
li 1, 314
write 1
halt
Recall that the program counter
PC is used to hold the address of
the current instruction being executed.
After the instruction whose address is in
PC is executed, the
value in
PC is incremented by one.
Registers with truth values along with
conditional jump instructions are used to
determine whether control should jump to an instruction
other
than
PC + 1.
Suppose we want a program to exhibit the following behavior:
If the value in register 6 is greater than or equal to the value in
register 5, then execute the instruction whose location is in
register 8
We would use a combination of an arithmetic comparison instruction and
a
conditional jump instruction:
slt 4, 6, 5 ; set reg4 to 1 if reg6 < reg5
jeqz 4, 8 ; jump to the location in reg8
; if reg4 = 0, i.e. reg6 >= reg5
General form of the conditional jump:
jeqz sourcereg, addressreg
Meaning: Jump to the location in
addressreg if
sourcereg contains
false (0).
The
jeqz instruction can be interpreted as "jump on false."
If you want to do something
X on a certain condition, then:
- Use a comparison instruction that sets its register on
the negation (opposite) of that condition, and
- Use jeqz to jump to a location in instruction memory that
does X.
In the previous example:
- The condition is that reg6 ≥ reg5
- The compare instruction is slt 4, 6, 5
- The location in memory to do X is in reg4
Suppose instruction memory, the PC, and certain registers are in the
following state:

Suppose that before the
slt instruction is executed, registers 5
and 6 have the values as shown:

The PC will automatically be incremented to
99.
Since register 6 < register 5, register 4 will be set to
1:

The PC will automatically be incremented to
100.
Since register 4 is not
0, the PC stays at
100:

Suppose that before the
slt instruction is executed, registers 5
and 6 have their values reversed:

The PC will automatically be incremented to
99.
Since register 6 ≥ register 5, register 4 will be set to
0:

The PC will automatically be incremented to
100.
Since register 4 is
0, the PC gets the contents of register 8 (
200):

Sometimes, "unconditional" jumps are used:
j addressreg
Meaning: "Jump to the location in
addressreg no matter
what."
This section explains how symbolic names make assembly language
programs easier to write and understand.
Consider a program that reads in two numbers and then uses conditional
jumping to display the larger of the two.
The flow chart below shows the program's structure:

read 1 ; read input into registers 1 and 2
read 2
sge 3, 1, 2 ; set reg 3 to 1 if reg 1 ≥ reg 2, otherwise 0
li 4, 7 ; 7 is address of the "write 2" instruction, for jump
jeqz 3, 4 ; if reg 1 < reg 2, jump to instruction 7 (write 2)
write 1 ; reg 1 ≥ reg 2, so write reg 1 and halt
halt
write 2 ; reg 1 < reg 2, so write reg 2 and halt
halt
- We must remember which registers are used for which
purposes
- We must figure out the instruction number (i.e., the address in instruction
memory) of the jump target for the jeqz instruction (see
right)
These difficulties are significant for large programs that are edited frequently.
Many assembly languages (including SLIM) allow names for:
- Register assignment
- Labeling points within the program for use as jump targets
In SLIM,
- Register assignment is accomplished with
the allocate-registers declaration.
- A program location is named by inserting a label followed by a colon
allocate-registers input-1, input-2
allocate-registers comparison, jump-target
read input-1
read input-2
sge comparison, input-1, input-2
li jump-target, input-2-larger
jeqz comparison, jump-target
write input-1
halt
input-2-larger:
write input-2
halt
Note that blank lines and spaces can be used to emphasize program structure.
Recall the
Recursion Strategy:
Do nearly all the work first on a self-similar, smaller problem; then
there will only be a little left to do.
And the
Iteration Strategy:
Progressively reduce a problem to another problem that gives the
same result.
At the beginning of this course, recursion was presented before
iteration because recursion is easily implemented in Scheme.
When programming in assembly language (SLIM), iteration is easier to
implement due to the availability of
jump instructions.
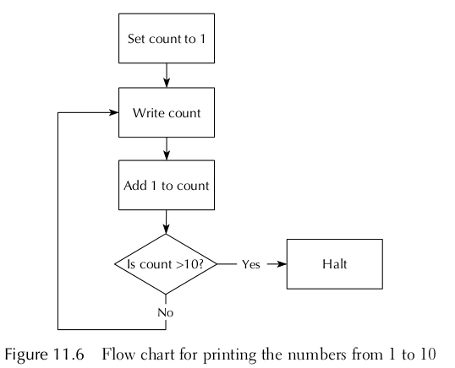
The flow chart below shows the control structure for a
program that prints the numbers from 1 to 10.
To implement the program in SLIM, we will use registers for three purposes:
- Holding varying quantities, like count
- Holding constant values, like 1 and 10
- Holding program locations for the purpose of jumping
Note how the SLIM program and the flow chart parallel each other:
allocate-registers count, one, ten
allocate-registers loop-start, done
li count, 1
li one, 1
li ten, 10
li loop-start, the-loop-start
the-loop-start:
write count
add count, count, one
sgt done, count, ten
jeqz done, loop-start
halt
|

|
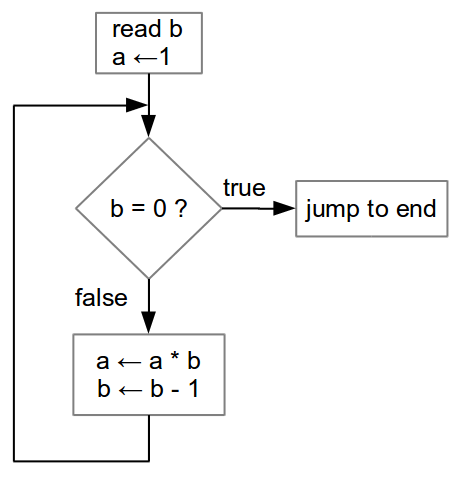
Recall the Scheme program for iteratively computing factorial:
(define factorial-product
(lambda (a b) ; computes a * b!, provided
(if (= b 0) ; b is a nonnegative integer
a
(factorial-product (* a b) (- b 1)))))
(define factorial
(lambda (n)
(factorial-product 1 n)))
The SLIM program for
factorial will use registers for similar
purposes:
- Holding varying quantities a and b
- Holding the constant value 1
- Holding program locations for the purpose of jumping
One of the registers used for jumping is called a
continuation
register because it holds an address of code to execute when the
iteration is complete.
Suppose register
b has a non-negative integer.
A flow chart for computing
b! in register
a,
where
end is a continuation register appears to the right.
Note that the flow chart includes algorithmic "pseudocode" that is not
executable but indicates common arithmetic operations and data
movements. For example, if
a and
b are registers, then
a ← a * b
is pseudocode for the SLIM instruction
mul a, a, b
allocate-registers a, b, one, factorial-product, end
li a, 1
read b
li one, 1
li factorial-product, factorial-product-label
li end, end-label
factorial-product-label:
;; computes a * b! into a and then jumps to end
;; provided that b is a nonnegative integer;
;; assumes that the register named one contains 1 and
;; the factorial-product register contains this address;
;; may also change the b register’s contents
jeqz b, end ; if b = 0, a * b! is already in a
mul a, a, b ; otherwise, we can put a * b into a
sub b, b, one ; and b - 1 into b, and start the
j factorial-product ; iteration over
end-label:
write a
halt
This section presents a more interesting use of continuation registers
in SLIM.
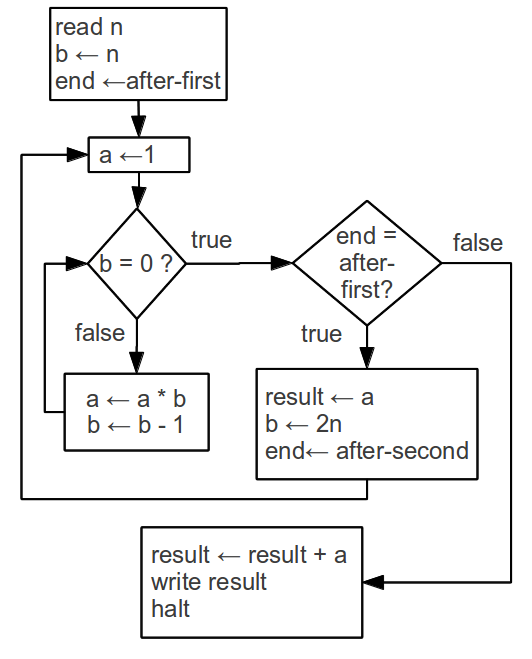
Consider the following computation of
n! + (2n)! in Scheme:
(define factorial-product ; unchanged from before
(lambda (a b) ; computes a * b!, given b is a nonnegative integer
(if (= b 0)
a
(factorial-product (* a b) (- b 1)))))
(define two-factorials
(lambda (n)
(+ (factorial-product 1 n)
(factorial-product 1 (* 2 n)))))
read n
b ← n
end ← after-first
loop to compute b! in a
after-first:
result ← a
b ← 2n
end ← after-second
loop to compute b! in a
after-second:
result ← result + a
write result
halt
allocate-registers a, b, one, factorial-product
allocate-registers end, n, result, zero ; note new registers
li one, 1
li zero, 0
li factorial-product, factorial-product-label
read n
li a, 1
add b, zero, n ; copy n into b by adding zero
li end, after-first ; note continuation is after-first
factorial-product-label: ; same loop as before
jeqz b, end
mul a, a, b
sub b, b, one
j factorial-product
after-first:
add result, zero, a ; save n! away in result
li a, 1
add b, n, n ; and set up to do (2n)!,
li end, after-second ; continuing differently after
j factorial-product ; this 2nd factorial-product,
after-second: ; namely, by
add result, result, a ; adding (2n!) in with n!
write result ; and displaying the sum
halt
Recall the Scheme procedure for recursively computing factorial:
(define factorial
(lambda (n)
(if (= n 0)
1
(* (factorial (- n 1)) n))))
And the
Recursion Strategy:
Do nearly all the work first on a self-similar, smaller problem; then
there will only be a little left to do.
Q: How to implement recursion in SLIM?
Recall the Scheme trace of
(factorial 5):
> (factorial 5)
>(factorial 5) ; remember 5, compute 4!
> (factorial 4) ; remember 4, compute 3!
> >(factorial 3) ; remember 3, compute 2!
> > (factorial 2) ; remember 2, compute 1!
> > >(factorial 1) ; remember 1, compute 0!
> > > (factorial 0) ; base case
< < < 1 ; 0! = 1
< < <1 ; 1! = 1 × 0! = 1
< < 2 ; 2! = 2 × 1! = 2
< <6 ; 3! = 3 × 2! = 6
< 24 ; 4! = 4 × 3! = 24
<120 ; 5! = 5 × 4! = 120
120
A SLIM program must represent the
data values:
- n: the argument
- val: an intermediate value 1, 2, 6, 24, ...
and the
program locations:
- after-recursive-invocation: code to compute the intermediate
value val and continue computation
- after-top-level: code to write the final result and halt
While other values and locations will be required, these are critical to a
recursive implementation.
Not only must
n be remembered when a recursive invocation is
executed, but the program location to continue with after must also be remembered:
> (factorial 5)
>(factorial 5) ; remember after-top-level
> (factorial 4) ; remember after-recursive-invocation
> >(factorial 3) ; remember after-recursive-invocation
> > (factorial 2) ; remember after-recursive-invocation
> > >(factorial 1) ; remember after-recursive-invocation
> > > (factorial 0) ; remember after-recursive-invocation
< < < 1 ; 0! = 1, continue at after-recursive-invocation
< < <1 ; 1! = 1 × 0!, continue at after-recursive-invocation
< < 2 ; 2! = 2 × 1!, continue at after-recursive-invocation
< <6 ; 3! = 3 × 2!, continue at after-recursive-invocation
< 24 ; 4! = 4 × 3!, continue at after-recursive-invocation
<120 ; 5! = 5 × 4!, continue at after-top-level
120
Two values must be remembered across recursive invocations of
SLIM
factorial:
- The argument n — suppose it is stored in
register n
- The program location after-top-level (ATL)
or after-recursive-invocation (ARI) — suppose it is
stored in register cont
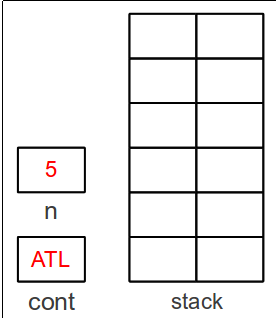
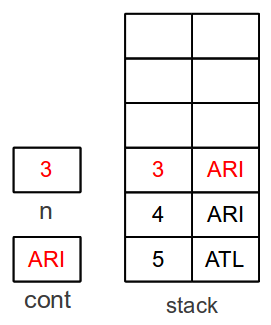
To compute
5!, we store
5 in
n and
ATL
in
cont, and we create an empty stack:
This section describes the use of the stack to recurse down to the base case.
5! will be computed as
5 × 4!.
To compute
4!, the values in
n (5) and
cont (ATL)
will be saved on the stack.
Now
n can be loaded with new value
n - 1 (4).
After computing
4!, computation must continue
at
after-recursive-invocation (ARI), so
cont is set
to
ARI.
4! will be computed as
4 × 3!.
To compute
3!, the values in
n (4) and
cont (ARI)
will be saved on the stack.
Again, new values will be loaded into
n
and
cont and pushed.
The pushing process continues as long as
n does not
equal
0.
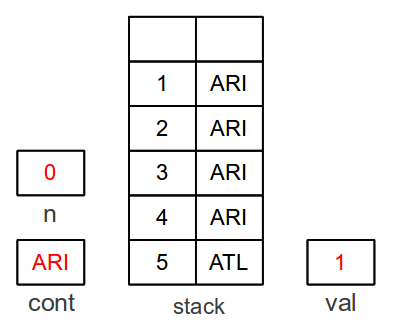
When
n = 0, the push loop stops and
0! = 1 is stored
in a register,
val, that will accumulate products.
If the top-level call had been
0!, then
cont would
contain
ATL (after-top-level), and we would be done.
Instead, we were in the process of a recursive invocation
(computing
1! as
1 × 0!), so we must
complete the computation by executing the following instructions at the
location
ARI (after-recursive-invocation):
- Pop saved values on the stack into cont and n
- Multiply val by n and store the result back
into val, and
- Return to the program location stored in cont
This process is repeated any time the location stored in
cont
is
ARI (after-recursive-invocation).
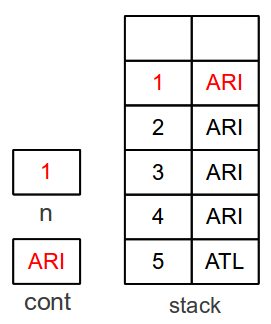
The first time we enter the code at
ARI:
- Pop stack value ARI into cont and 1
into n
- val ← val × n ; n=1
- Continue processing at the value in cont (ARI)
The second time we enter the code at
ARI:
- Pop stack value ARI into cont and 2
into n
- val ← val × n ; n=2
- Continue processing at the value in cont (ARI)
The third time we enter the code at
ARI:
- Pop stack value ARI into cont and 3
into n
- val ← val × n ; n=3
- Continue processing at the value in cont (ARI)
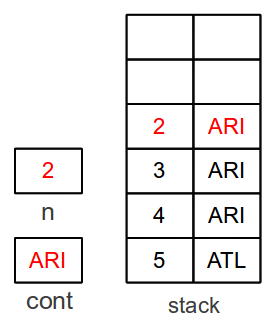
The fourth time we enter the code at
ARI:
- Pop stack value ARI into cont and 4
into n
- val ← val × n ; n=4
- Continue processing at the value in cont (ARI)
The fifth time we enter the code at
ARI:
- Pop stack value ATL into cont and 5
into n
- val ← val × n ; n=5
- Continue processing at the value in cont (ATL)
Since
cont contains
ATL, stack processing is complete and
the result of the top-level call
5! is stored in
val.
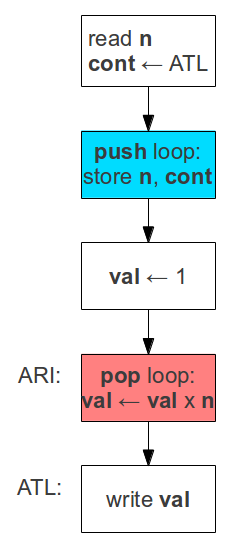
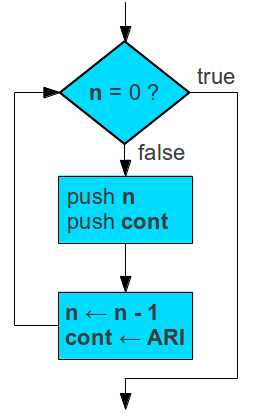
A top-level flow chart for the recursive SLIM implementation
of
factorial is shown below.
Most of the work is performed by the
push and
pop loops,
shown next.
Note that the test
cont = ATL, after the initial setting
of
val to
1, is necessary in case the original value read
into
n is
0. (What would happen if the test were omitted
and control passed immediately to the pop loop?)
Since SLIM has a (relatively) limited number of registers, a stack will
be implemented in data memory.
We visualize the bottom of the stack at location
0, with
memory addresses increasing from bottom to top.
To access the stack, we use a register
sp that acts as
a
stack pointer, holding the address of the next available
location in the stack.
A representation of an empty stack is shown to the right.
To push onto the stack, we use the
store instruction:
st sourcereg, addressreg
To prepare for the first recursive invocation in the computation
of
5!:

To pop from the stack, we use the
load instruction:
ld destreg, addressreg
Suppose we have reached the base case in
factorial and are ready
to begin the pop loop:

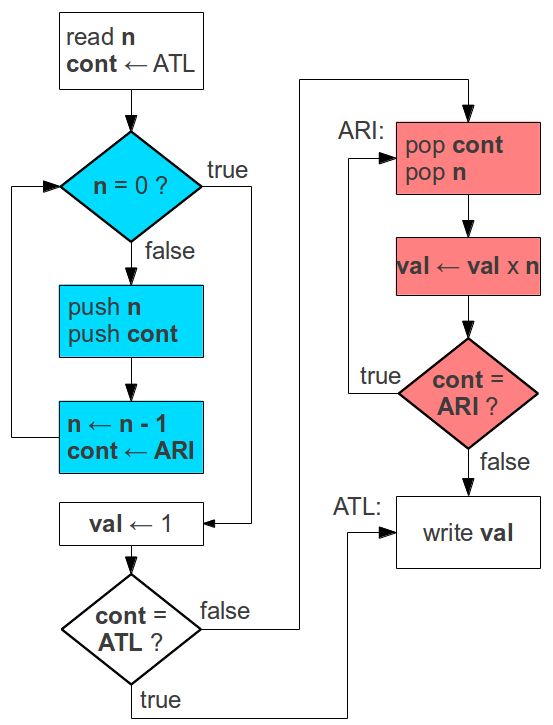
The SLIM code for factorial divides into code for:
- Register use and initialization
- Push loop
- Base case
- Pop loop
- Finish
allocate-registers n, cont ; the argument, continuation,
allocate-registers val ; and result of factorial procedure
allocate-registers factorial, base-case ; hold label values
allocate-registers sp ; the stack pointer
allocate-registers one ; the constant 1, used in several places
li one, 1 ; set up the constants
li factorial, factorial-label ; top of push loop
li base-case, base-case-label ; base case code
li sp, 0 ; initialize the stack pointer
read n ; the argument, n, is read in
li cont, after-top-level ; the continuation is set
factorial-label: ; computes the factorial of n into val
jeqz n, base-case
st n, sp ; push n onto stack
add sp, sp, one
st cont, sp ; push cont
add sp, sp, one
sub n, n, one ; using n-1 as the new n argument
li cont, after-recursive-invocation
j factorial ; continue the push loop
base-case-label: ; this is the n = 0 case
li val, 1
j cont
after-recursive-invocation:
sub sp, sp, one
ld cont, sp ; pop stack into cont
sub sp, sp, one
ld n, sp ; pop stack into n
mul val, val, n ; compute n! as (n-1)! * n,
; i.e. val * n,
j cont ; jump to the continuation
after-top-level: ; after top-level call,
write val ; display the result
halt
allocate-registers n, cont ; the argument, continuation,
allocate-registers val ; and result of factorial procedure
allocate-registers factorial, base-case ; hold label values
allocate-registers sp ; the stack pointer
allocate-registers one ; the constant 1, used in several places
li one, 1 ; set up the constants
li factorial, factorial-label
li base-case, base-case-label
li sp, 0 ; initialize the stack pointer
read n ; the argument, n, is read in
li cont, after-top-level ; the continuation is set
factorial-label: ; computes the factorial of n into val
jeqz n, base-case
st n, sp ; push n onto stack
add sp, sp, one
st cont, sp ; push cont
add sp, sp, one
sub n, n, one ; using n-1 as the new n argument
li cont, after-recursive-invocation
j factorial ; continue the push loop
after-recursive-invocation:
sub sp, sp, one
ld cont, sp ; pop stack into cont
sub sp, sp, one
ld n, sp ; pop stack into n
mul val, val, n ; compute n! as (n-1)! * n, i.e. val * n,
j cont ; jump to the continuation
base-case-label: ; this is the n = 0 case
li val, 1
j cont
after-top-level: ; after top-level call,
write val ; display the result
halt










































 Note that the test cont = ATL, after the initial setting
of val to 1, is necessary in case the original value read
into n is 0. (What would happen if the test were omitted
and control passed immediately to the pop loop?)
Note that the test cont = ATL, after the initial setting
of val to 1, is necessary in case the original value read
into n is 0. (What would happen if the test were omitted
and control passed immediately to the pop loop?)




