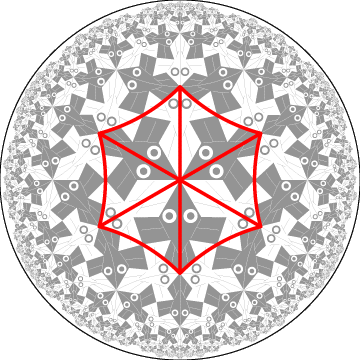
Figure 3: Six isosceles triangles superimposed on Escher's
Circle Limit I pattern.
The program has been extended slightly so that this modification
is often not necessary. The extended program also seems to work
reasonably well with a motif that overlaps two adjacent isosceles
triangles (with roughly half the motif in each triangle)
- as is
the case with Circle Limit IV
(Figure 1).
The basic transformation process makes use of the Klein model of
hyperbolic geometry. As with the
Poincaré
model, the points are interior points of a bounding circle, but the
hyperbolic lines are represented by chords. We let
I
denote the isomorphism that maps the
Poincaré
model to the Klein model. Then
I
maps a centered
p-gon
with its isosceles triangles to a regular
p-sided
polygon which also contains corresponding isosceles triangles.
Different tessellations
{p,q}
produce different isosceles triangles in the Klein model,
but an isosceles triangle from
{p,q}
can be mapped onto an isosceles triangle from
{p',q'}
by a simple (Euclidean) differential scaling, since those isosceles
"Klein" triangles are represented by isosceles Euclidean triangles.
Thus the transformation from a
{p,q}
pattern to a
{p',q'}
pattern can be accomplished by
(1) applying
I
to a motif in an isosceles triangle of
{p,q},
(2) applying the differential scaling to that transformed triangle, and
finally
(3) applying the inverse of
I
to the re-scaled triangle containing the motif.
The entire pattern can then be formed by replicating the transformed motif.
Replication algorithms are discussed in Dunham
(1986a) and Dunham
(1986b).
Figure 4
shows the result of transforming the
Circle Limit I
pattern to a {4,6} pattern -
with a transformed isosceles triangle
superimposed.
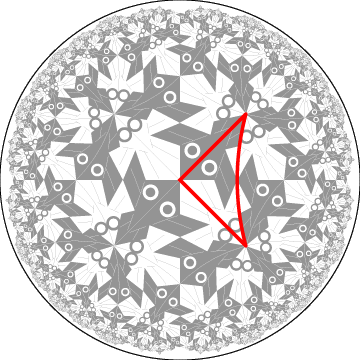
Figure 4: A transformed
Circle Limit I
based on {4,6} showing one isosceles triangle.
Using similar techniques, another program has been written to
transform isosceles Euclidean triangles to isosceles hyperbolic triangles,
and thus Euclidean Escher patterns (of which there are many) can be
transformed to hyperbolic patterns.