1. Developing a Dodecaphonic Row. The central concept behind dodecaphony is the notion that all of the music should arise from a single compositional element: the 12-tone row. A tone row (or series), as prescribed by Schönberg, must contain each of the twelve chromatic pitches (called a pitch class) once and only once. This avoidance of repetition is construed so that there is no sense that any pitch has more weight than another (to contrast with the major/minor key system wherein there exists a clear hierarchy within the relationships between pitches, such as the tonic, dominant, mediant, etc.). Rather than using the term atonal, which can have a negative connotation, Schönberg employed the term pantonal to describe the listening experience (which is also often referred to as non-tonal).
The tone row is the initial point of departure for the composer, and as such can be created simply from a melodic idea. However, many composers choose to construct a row from an abstract interval-based concept before composing, in the true sense, begins. To intensify the tightly knit approach of using a tone-row, the series can be broken down into interrelated groups containing similar constructs within themselves. For instance, two groups of six notes (called hexachords) or three groups of four notes (called tetrachords) can be arranged as long as there is no repetition of pitches between the groups.
For our purposes, we will create a series from two hexachords. Note that we have carefully devised a sequence of intervals within the first hexachord (m3, M2, m2, tritone, m2) that is duplicated in the second (despite some directional differences). The two hexachords are additionally related by the tritone (C-F#) - an interval regarded by some composers as an axis of non-tonal music similar to the tonic/dominant relationship of tonal practices.
There are many varied approaches to creating tone rows based on an abstract pre-compositional idea, such as series that contain all intervals, others that have some extra-musical significance (based on letters of names, etc.), or those that actually have tonal implications (such as triadic construction or scalar material). Each composer should develop their rows based on the expressive needs of the piece at hand; it is a more flexible system than many practitioners and those in the Academy admit.
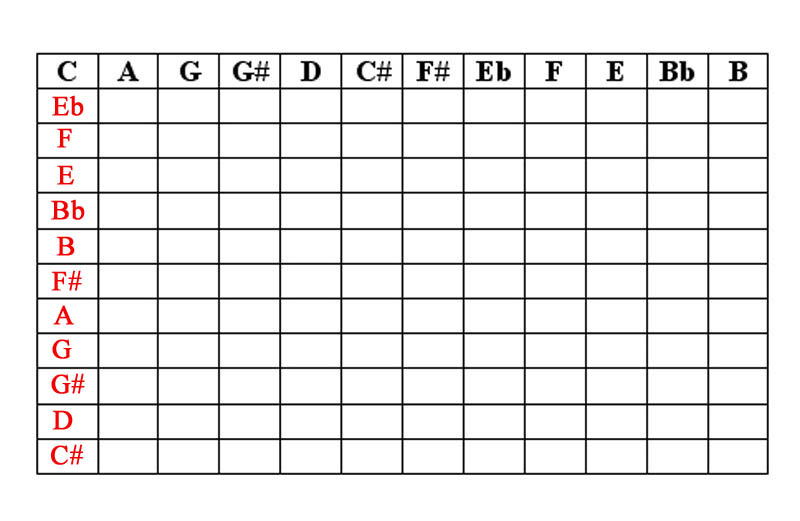
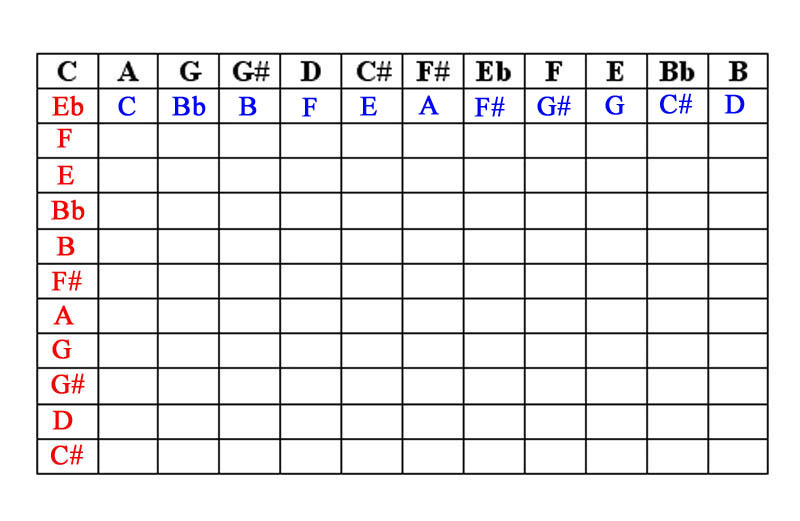
2. Dodecaphonic Inversions. The next essential 12-tone principle maintains the idea that any piece of musical material can be articulated in its original version (referred to henceforth as its prime) as well as its inversion wherein the direction of each interval is reversed (e.g. an ascending minor third in the prime will become a descending minor third in the inversion). To derive the inversion of a row, we can create a chart (here based on the first note of the row we have created). Based on the illustrated below, the inversion of our prime row would read: C, Eb, F, E, Bb, B, F#, A, G, G#, D, C#.
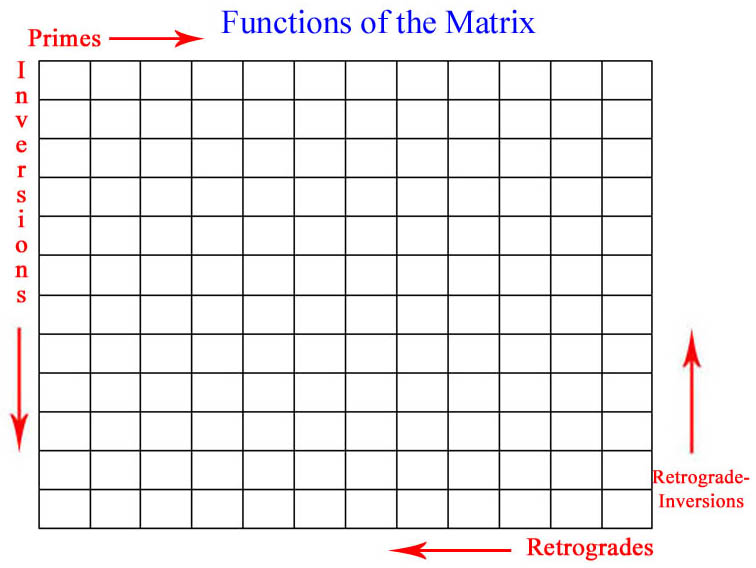
3. The Four Basic Forms. In addition to the prime and inversion forms, each row can be articulated from last pitch to first, a transformation called retrograde. As applied to the inversion form of the row, this is called retrograde-inversion. As such, the rows notated below illustrate the four basic forms of our original series. Note that we have added an accidental before each note, regardless if it seems to need a natural or not. This stems from Schönberg's practice to avoid any ambivalence in the total-chromatic field.
Also, it is important for the student to realize that without any tonal hierarchy, there exists no functional difference between, say, C# and Db or G# and Ab. The preference between the two will depend on the situation in the actual composition and what is clearest for the performer to read. With this in mind, some theorists substitute numbers 0-11 for the pitch names. Although this is useful for analytical purposes, for our compositional needs we will preserve the traditional note names.
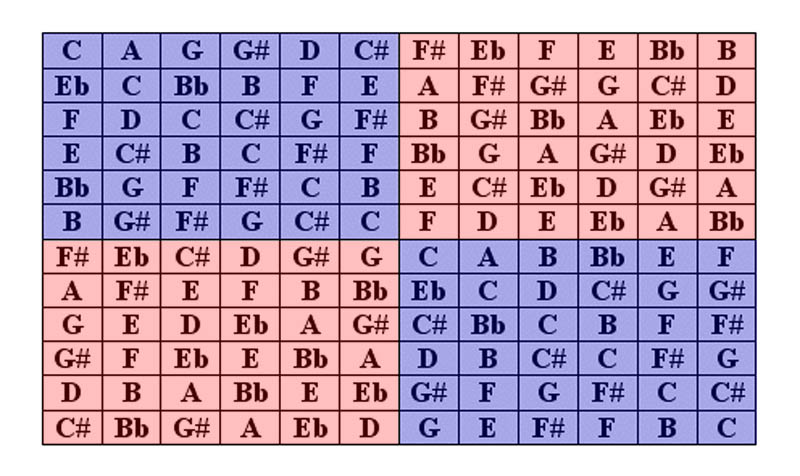
4. The Dodecaphonic Matrix. As we have observed, dodecaphony inherits an important premise from the Renaissance composers' ideal to create with an economy of means in order to provide a unified and organic artistic expression, or more simply put, as much musical development possible from as little primary material possible. As such, Schönberg devised a visual way for the composer to examine all possible versions of a given row by borrowing an idea from mathematics: the matrix. This should by no means be interpreted that 12-tone music is somehow inordinately 'mathematical', just as artists outlining horizon lines to organize perspective in a painting should as well not be so accused.
5. Extrapolating a Matrix from a Row: Inversions. After inserting our original prime series as the first row in the matrix, reading from left to right; the inversion of this row can be inserted reading down in the first column.
6. Extrapolating a Matrix from a Row: Transpositions. The final step to creating our matrix is the simple task of deriving the transpositions.
7. Complete Matrix. The final version of our matrix will feature all of the forty-eight transformations (four basic forms, twelve transpositions each) that can be derived from the original row. To make viewing easier, we have used contrasting colors to clearly distinguish adjoining hexachords.
Continue for methods to develop compositions using selected dodecaphonic techniques.