
|
Figure 1: A rendition of Escher's hyperbolic pattern
Circle Limit IV
of angels (the white background) and devils (foreground).
|
There are probably many ways to distort or transform one pattern into
another. The method we will describe applies to repeating patterns
based on the regular tessellations,
{p,q},
composed of regular
p-sided polygons meeting
q at a vertex.
Thus, given one repeating pattern, we could theoretically create a
doubly infinite family of related patterns by transforming the original
pattern into others based on different values of
p and q.
Many of Escher's Euclidean patterns and all of his spherical and
hyperbolic patterns are based on
{p,q}.
For example, his Euclidean Notebook Pattern Number 45
and the related spherical
and hyperbolic patterns mentioned above are based on the tessellations
{4,4},
{4,3}, and
{6,4} respectively.
Figure 2 below shows
the tessellation {6,4} superimposed on the
Circle Limit IV pattern.
In these patterns,
p
is twice the number of angels/devils that meet at their feet and
q
is the number of wing tips that meet at a point.
The meeting point of feet is the intersection of lines of bilateral
(reflection) symmetry - hence the need to double the number of
angels/devils to obtain p.
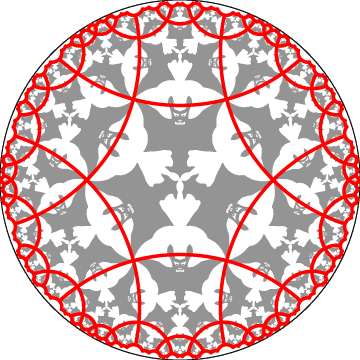
Figure 2: The Circle Limit IV pattern
showing the underlying {6,4} tessellation.
We will begin with a brief review of hyperbolic geometry.
Then we discuss repeating patterns and regular tessellations, and
the transformation process, showing an example.
Next we will show other examples based on Escher's four hyperbolic
patterns. Finally we suggest possible further directions of research.